Code is copied!
CLASS 12 ISC - Java Question Paper 2023
Maximum Marks: 70
Time Allowed: Three hours
(Candidates are allowed additional 15 minutes for only reading the paper.)
(They must NOT start writing during this time).
Answer all questions in Part I (compulsory) and six questions from Part-II,
choosing two questions from Section-A, two from Section-B and
two from Section-C.
All working, including rough work, should be done on the same sheet as the
The intended marks for questions or parts of questions are given in brackets [ ]
PART I
(Attempt all questions)
Question 1
(i)
According to De Morgan's law (a + b +c’ )' will be equal to:
(a) a' + b' + c’
(b) a' + b'+c
(c) a'.b'.c'
(d) a'b'c
(ii)
The dual of (X'+ 1 ).(Y' + 0) = Y'
(a) X.0 + Y.1 = Y
(b) X'.1 + Y'.0 = Y'
(c) X'.0 + Y'.1 = Y'
(d) (X'+ 0) . (Y'+ 1) = Y'
(iii)
The reduced expression of the Boolean function F(P,Q) =P’ + PQ is:
(a) P' + Q
(b) P
(c) P'
(d) P+Q
(iv)
If (~p => ~q ) then its contra positive will be:
(a) p=>q
(b) q=>p
(c) ~q=>p
(d) ~p=>q
(v)
The keyword that allows multi-level inheritance in Java programming is:
(a) implements
(b) super
(c) extends
(d) this
Question 2
(ii) A matrix M[-6...10, 4...15] is stored in the memory with each element requiring 4 bytes of storage. If the base address is 1025, find the address of M[4][8] when the matrix is stored in Column Major Wise.
(iii)
With reference to the code given below, answer the questions that follow along
with dry run / working.
boolean num(int x)
{
int a=1;
for (int c=x; c>0; c/=10)
a * = 10;
return (x * x % a) == x;
}
(a) What will the function num() return when the value of x=25?
(b) What is the method num() performing?
(iv)
The following function task(Q) is a part of some class. Assume ‘m’ and ‘n’ are positive integers, greater than 0. Answer the questions given below along with dry run / working.
int task(int m, int n)
{ if(m==n)
retum m;
else if(m>n)
return task(m-n, n);
else
retum task(m, n-m);
}
(a) What will the function task() return when the value of m=30 and n=45?
(b) What function does task() perform, apart from recursion?
PART II
SECTION - A
(Answer any two questions.)
Question 3
(i) Given the Boolean function F(A,B,C,D) = ∑(2, 3, 6, 7, 8, 10, 12, 14, 15).
(a) Reduce the above expression by using 4-variable Karnaugh map, showing
the various groups (i.e., octal, quads and pairs).
(b) Draw the logic gate diagram for the reduced expression. Assume that the
variables and their complements are available as inputs.
(ii) Given the Boolean function F(A,B,C,D) = π(0, 1, 2, 4,5, 8, 10, 15, 14, 15),
(a) Reduce the above expression by using 4-variable Karnaugh map, showing
the various groups (i.e., octal, quads and pairs).
(b) Draw the logic gate diagram for the reduced expression. Assume that the
variables and their complements are available as inputs
(i) A shopping mall allows customers to shop using, cash or credit card of any
nationalised bank. It awards bonus points to their customers on the basis of
criteria given below:
- The customer is an employee of the shopping mall and makes the
payment using a credit card
OR
- The customer shops items which carry bonus points and makes the
payment using a credit card with a shopping amount of less than
Rs 10,000/-
OR
- The customer is not an employee of the shopping mall and makes the
payment not through a credit card but in cash for the shopping amount
above Rs 10,000/-
The inputs are:
C - Payment through a credit card
A - Shopping amount is above Rs 10,000/-
E - The customer is an employee of the shopping mall
I - Item carries a bonus point
(In all the above cases, 1 indicates yes and 0 indicates no.)
Output: X [1 indicates purchased, 0 indicates not purchased for all cases]
Draw the truth table for the inputs and outputs given above and write the POS
expression for X (C, A, E, I).
(ii) Differentiate between half adder and full adder. Write the Boolean expression and draw the logic circuit diagram for the SUM and CARRY of a full adder.
(iii) Verify the following expression by using the truth table:
(A ⊙ B)' = (A ⊕ B)
(i) What is an encoder? How is it different from a decoder? Draw the logic circuit for a 4:1 multiplexer and explain its working.
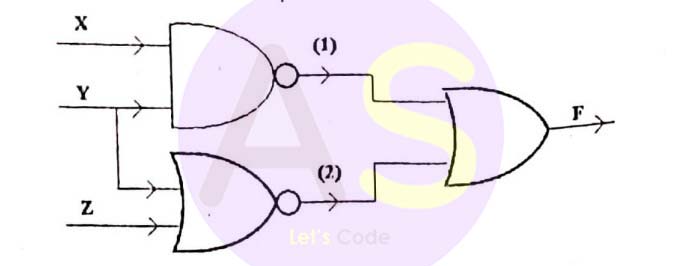
(ii) From the logic diagram given below write the boolean expression for (1) and (2). Also, derive the boolean expression (F) and simplify it:
(iii) Convert the following cardinal expression to its canonical form:
F (P, Q, R) = π(0, 1, 3, 4)

SECTION B
(Attempt all questions from this Section.)
Question 6
Design a class NumDude to check if a given number is a Dudeney number or not. (A Dudeney number is a positive integer that is a perfect cube, such that the sum of its digits is equal to the cube root of the number.)
Example: 5832 = (5+8+3+2)=(18)³ = 5832
Some of the members of the class are given below:
Class name : NumDude
Data member/instance variable:
num:to store a positive integer number
Methods/Member functions:
NumDude():default constructor to initialise the data member with legal initial value
void input():to accept a positive integer number
int sumDigits(int x):returns the sum of the digits of number 'x' using recursive technique
void isDude():checks whether the given number is a Dudeney number by invoking the function sumDigits() and displays the result with an appropriate message
Specify the class NumDude giving details of the constructor(), void input(), int sumDigits(int) and void isDude(). Define a main() function to create an object and call the functions accordingly to enable the task.
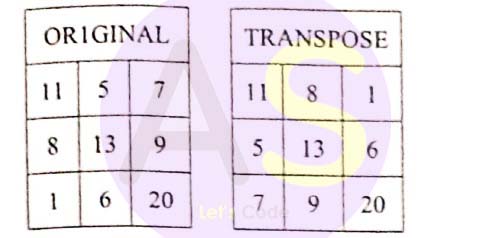
A class Trans is defined to find the transpose of a square matrix. A transpose of a matrix is obtained by interchanging the elements of the rows and columns.
Example: If size of the matrix = 3, then
 Some of the members of the class are given below:
Class name: Trans
Data members/instance variables:
arr[][]:to store integers in the matrix
m:integer to store the size of the matrix
Methods/Member functions:
Trans(int mm): parameterised constructor to initialise the data member m = mm
void fillarray():to enter integer elements in the matrix to create the transpose of the given matrix
void transpose():to create the transpose of the given matrix
void display():displays the original matrix and the transposed matrix by invoking the method transpose()
Specify the class Trans giving details of the constructor(), void fillarray(), void transpose() and void display(). Define a main() function to create an object and call the functions accordingly to enable the task.
Some of the members of the class are given below:
Class name: Trans
Data members/instance variables:
arr[][]:to store integers in the matrix
m:integer to store the size of the matrix
Methods/Member functions:
Trans(int mm): parameterised constructor to initialise the data member m = mm
void fillarray():to enter integer elements in the matrix to create the transpose of the given matrix
void transpose():to create the transpose of the given matrix
void display():displays the original matrix and the transposed matrix by invoking the method transpose()
Specify the class Trans giving details of the constructor(), void fillarray(), void transpose() and void display(). Define a main() function to create an object and call the functions accordingly to enable the task.
 Some of the members of the class are given below:
Class name: Trans
Data members/instance variables:
arr[][]:to store integers in the matrix
m:integer to store the size of the matrix
Methods/Member functions:
Trans(int mm): parameterised constructor to initialise the data member m = mm
void fillarray():to enter integer elements in the matrix to create the transpose of the given matrix
void transpose():to create the transpose of the given matrix
void display():displays the original matrix and the transposed matrix by invoking the method transpose()
Specify the class Trans giving details of the constructor(), void fillarray(), void transpose() and void display(). Define a main() function to create an object and call the functions accordingly to enable the task.
Some of the members of the class are given below:
Class name: Trans
Data members/instance variables:
arr[][]:to store integers in the matrix
m:integer to store the size of the matrix
Methods/Member functions:
Trans(int mm): parameterised constructor to initialise the data member m = mm
void fillarray():to enter integer elements in the matrix to create the transpose of the given matrix
void transpose():to create the transpose of the given matrix
void display():displays the original matrix and the transposed matrix by invoking the method transpose()
Specify the class Trans giving details of the constructor(), void fillarray(), void transpose() and void display(). Define a main() function to create an object and call the functions accordingly to enable the task.
A double ended queue is a linear data structure which enables the user to add and remove integers from either ends i.e., from front or rear. The details of the class deQueue are given below:
Class name: deQueue
Data members/ instance variables:
Qrr[]:array to hold integer elements
lim: maximum capacity of the dequeue
front: to point the index of the front end
rear:to point the index of the rear end
Methods/Member functions:
deQueue(int l):constructor to initialise lim= 1, front = 0 and rear = 0
void addFront(int v):to add integers in the dequeue at the front end if possible, otherwise display the message "OVERFLOW FROM FRONT"
void addRear(int v):to add integers in the dequeue at the rear end if possible, otherwise display the message "OVERFLOW FROM REAR"
int popFront():removes and returns the integers from the front end of the dequeue if any, else returns -999
int popRear(): removes and returns the integers from the rear end of the dequeue if any, else returns -999
void show():displays the elements of the dequeue
Specify the class deQueue giving details of the functions void addFront(int) and int popFront(). Assume that the other functions have been defined. The main() function and algorithm need NOT be written.
A super class Demand has been defined to store the details of the demands for a product. Define a subclass Supply which contains the production and supply details of the products.
The details of the members of both the classes are given below:
Class name: Demand
Data members/instance variables:
pid:string to store the product ID
pname:string to store the product name
pdemand: integer to store the quantity demanded for the product
Methods/Member functions:
Demand(...) : parameterised constructor to assign values to the data members
void display():to display the details of the product
Class name:Supply
Data members/instance variables:
pproduced: integer to store the quantity of the product produced
prate:to store the cost per unit of the product in decimal
Methods/Member functions:
Supply(...): parameterised constructor to assign values to the data members of both the classes
double calculation(): returns the difference between the amount of demand (rate x demand) and the amount produced(rate x produced)
void display():to display the details of the product and the difference in amount of demand and amount of supply by invoking the method calculation()
Assume that the super class Demand has been defined. Using the concept of inheritance, specify the class Supply giving the details of the constructor(...), double calculation() and void display().
The super class, main function and algorithm need NOT be written.
(i) A linked list is formed from the objects of the class given below
class Node
{
double sal;
Node next;
}
Write an Algorithm OR a Method to add a node at the end of an existing linked list. The method declaration is as follows:
void addNode(Node ptr, double ss)
(ii) Answer the following questions from the diagram of a Binary Tree given below:
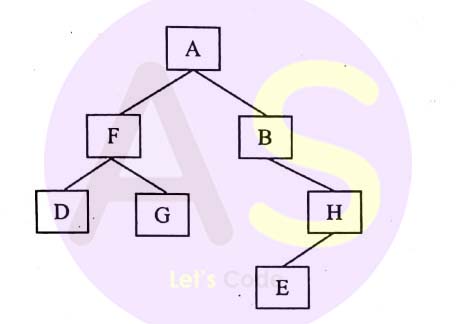 (a) Write the pre-order traversal of the above tree structure.
(b) Name the parent of the nodes D and B.
(c) State the level of nodes E and F when the root is at level 0.
(a) Write the pre-order traversal of the above tree structure.
(b) Name the parent of the nodes D and B.
(c) State the level of nodes E and F when the root is at level 0.
 (a) Write the pre-order traversal of the above tree structure.
(b) Name the parent of the nodes D and B.
(c) State the level of nodes E and F when the root is at level 0.
(a) Write the pre-order traversal of the above tree structure.
(b) Name the parent of the nodes D and B.
(c) State the level of nodes E and F when the root is at level 0.