Class 12 ISC- Java
Class 12th Java aims to empower students by enabling them to build their own applications introducing some effective tools to enable them to enhance their knowledge, broaden horizons, foster creativity, improve the quality of work and increase efficiency.
It also develops logical and analytical thinking so that they can easily solve interactive programs. Students learn fundamental concepts of computing using object oriented approach in one computer language with a clear idea of ethical issues involved in the field of computing
Class 12th java topics includes revision of class 11th, constructors, user-defined methods, objects and classes, library classes , etc.
Propositional Logic
Proposition is there an elementary atomic sentence that may either be true or false but not have other value.
Example :
1. Delhi is the capital of India.
2. Is Sita dancing ?
Types of Proposition
Simple Proposition : It is the one that does not contain any other proposition as a part. Example : Lucknow is the capital of Uttar Pradesh.
Compound Proposition : It is the one with two or more simple propositions as a part. Example : It is a hot day and I will drink cold drink.
Connectors
An Operator or connector joins two simple propositions into compound. There are basically three types of connectors :
1. Disjunction / Disjunctive (OR).
2. Conjunction / Conjunctive (AND).
3. Negation (NOT).
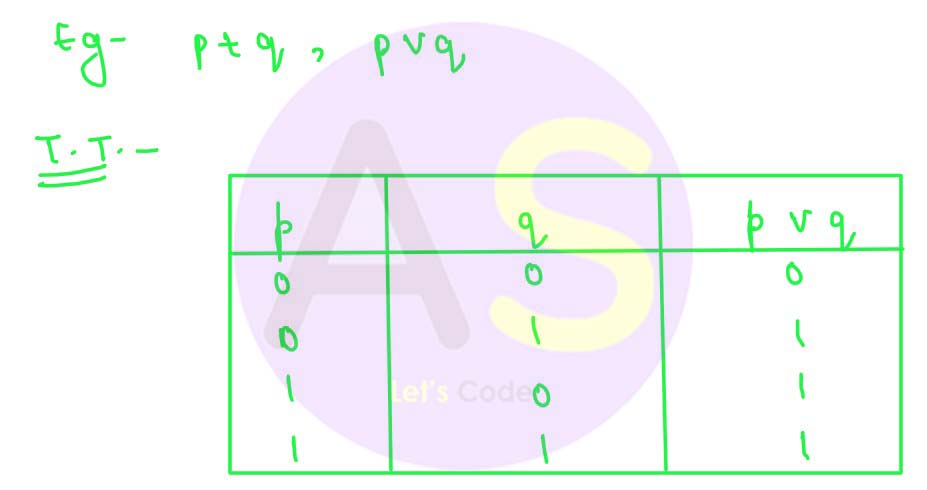
Disjunction (OR) : It is represented by (V) , + . It gives true if any of the one input is true otherwise false.

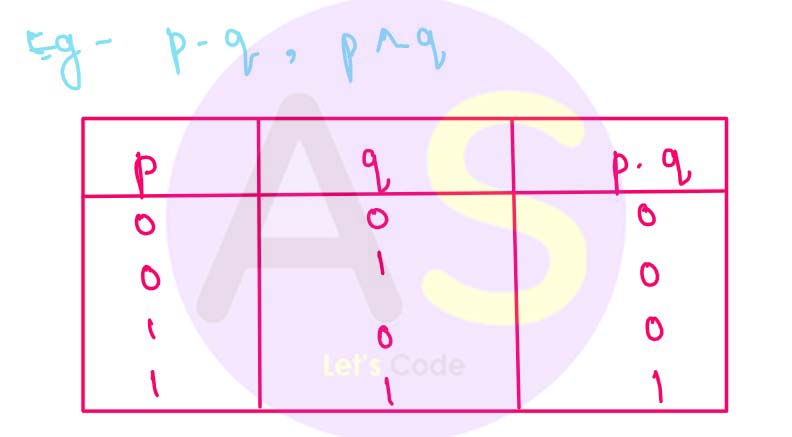
Conjunction (AND) : It is represented by (^) , (.) , It gives false if any of the one input is false otherwise true.

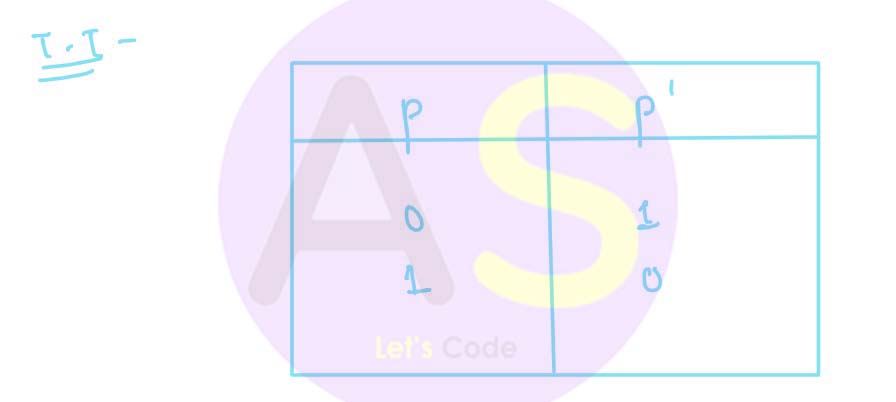
Negation (NOT) : It is represented by ~, - (overbar) , ' . Negation output will be false when p is true and vice versa.

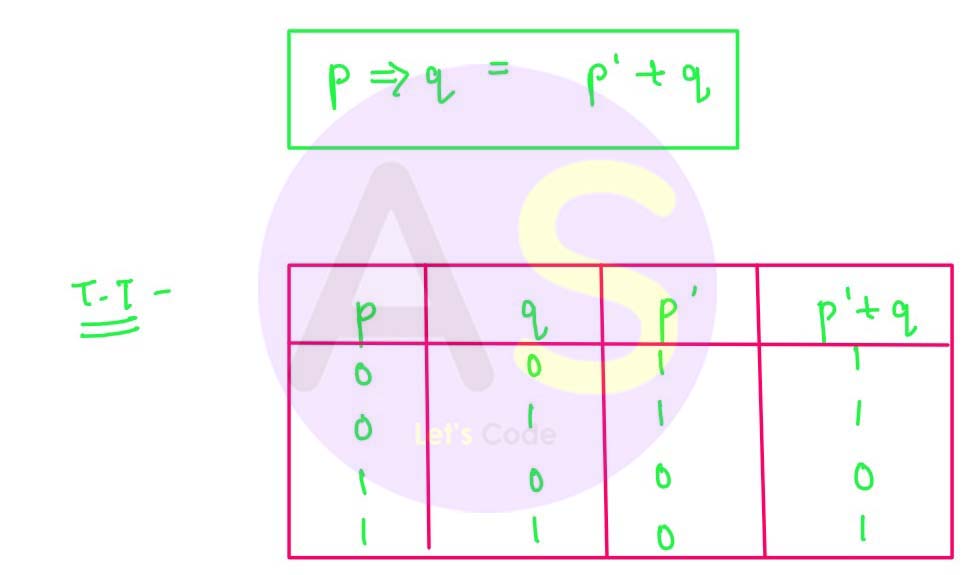
Conditional (Implication or If then)
It means p implication q will be false when p is true and q is false otherwise true. It is represented by →, ⇒, ⊃. Example : p→q , p⇒q, p ⊃ q

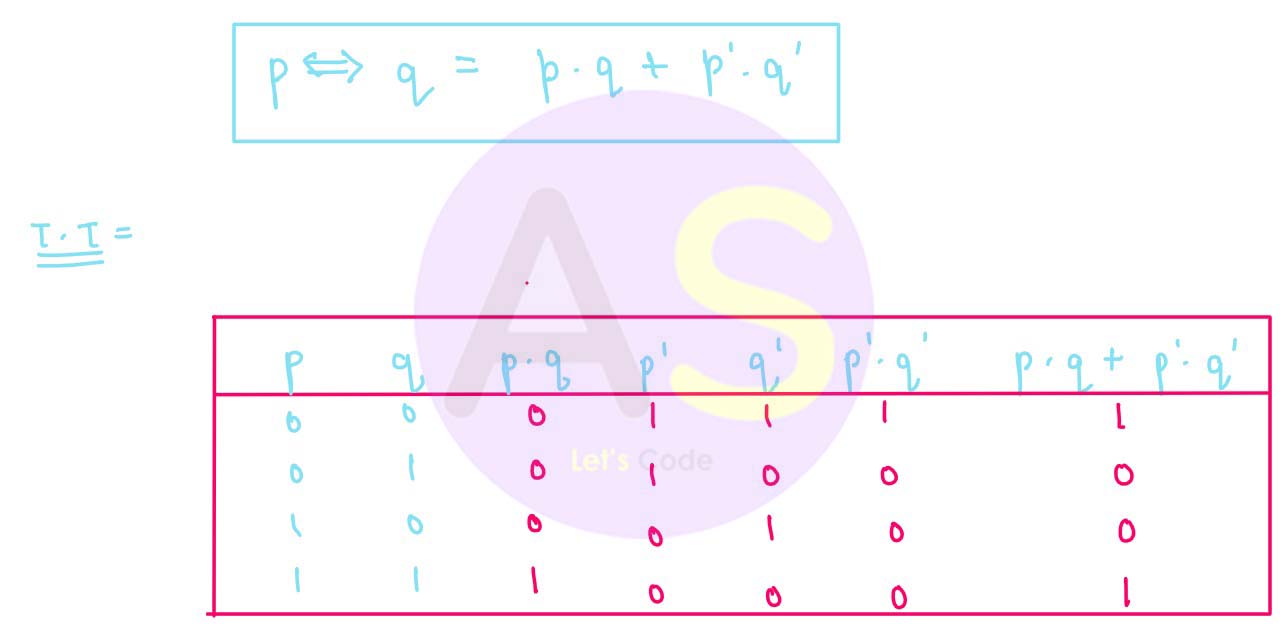
Biconditional (Equivalence or If and only if)
It means p ↔ q will be true when both the inputs are same otherwise false. It is represented by ⇔ , ↔ . Example : p↔q , p⇔q

Tautology
The propositions that have only 1's in their truth table output column is known as tautology.


Contradiction
The propositions that have only 0's in their truth table output column is known as contradiction.


Contingency
The propositions that have combinations of 0's and 1's in their truth table output column is known as contingency.


Converse
The converse of a conditional statement is interchanging of antecedent and consequent of any conditional statement
Example : p : you will work hard ; q : you will be rewarded
Converse : q ⇒ p - If you will be rewarded then you will work hard.

Inverse
The inverse of a conditional statement is obtained by negation of antecedent and consequent of any conditional statement

Example : p : it is raining ; q : sky is not clear
Inverse : ~p ⇒ ~q - If It is not raining the sky is clear.

Contrapositive
The contrapositive of a conditional statement is obtained by interchanging negation of antecedent and consequent of any conditional statement

Example : p : it is raining ; q : sky is clear
Contrapositive : ~q ⇒ ~p - If sky is not clear then it is not raining.

Some Practice Questions
1. State whether the following expressions are tautology contradiction or contingency.
1. (P ⇒ Q) V (Q ⇒ ~ P)

2. ~(P ⇒ Q) ⇔ (~P ⇒ Q)

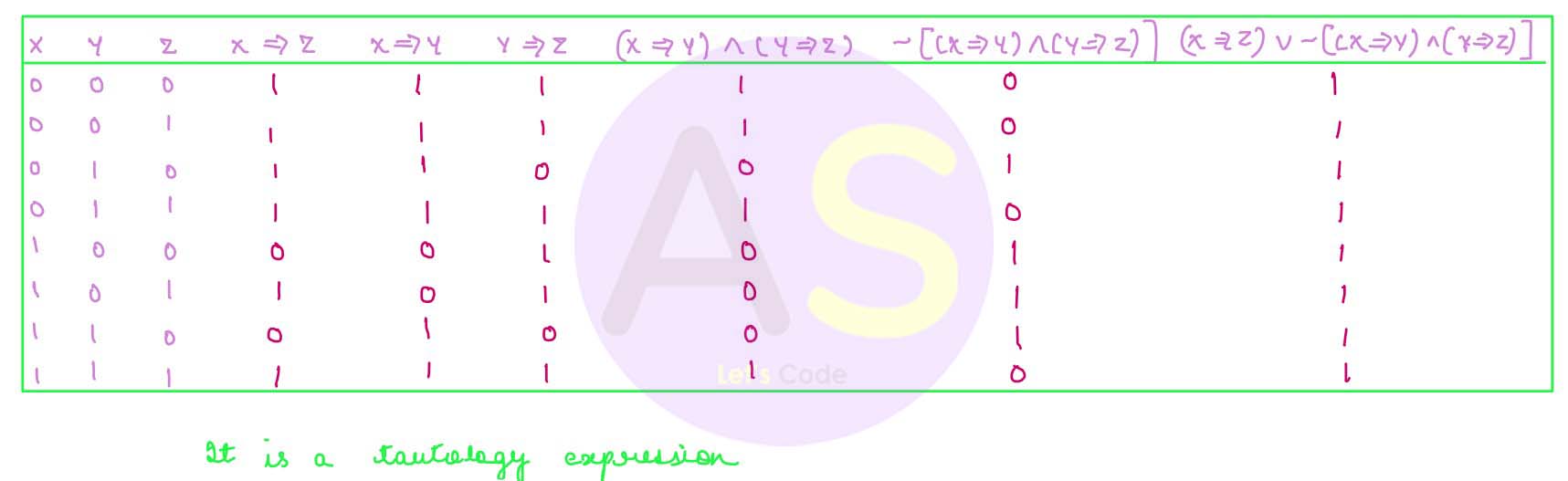
3. (X ⇒ Z) V ~[(X ⇒ Y) ^ (Y ⇒ Z)]
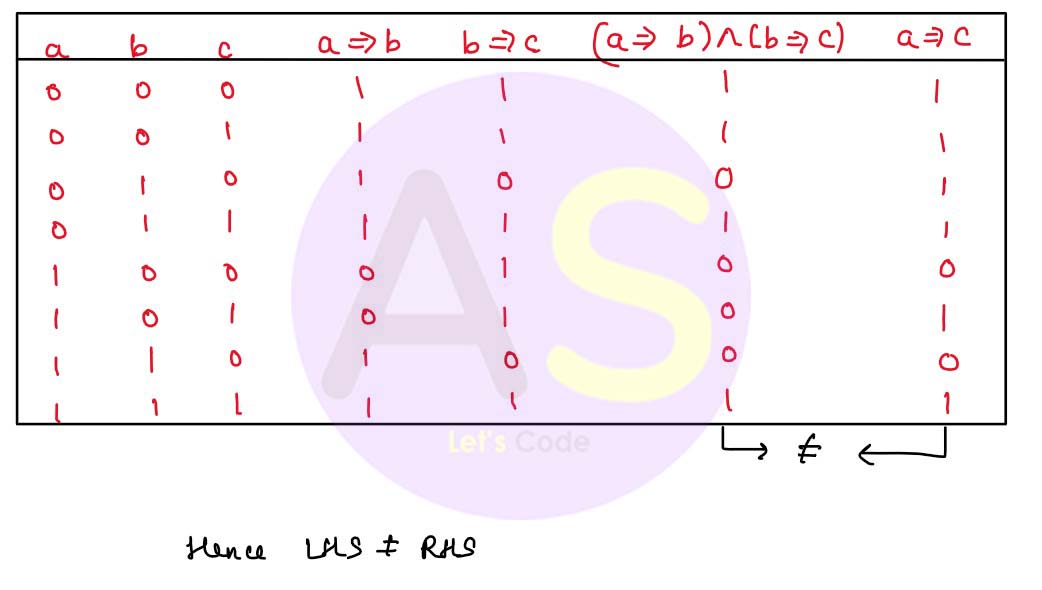
2. Verify the following with the help of truth table
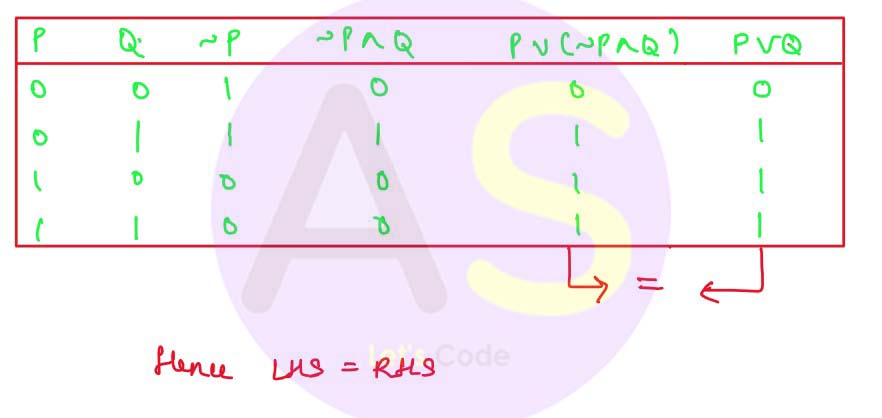
1. P V (~P ^ Q) = P V Q
2. (a ⇒ b) ^ (b ⇒ c) = (a ⇒ c)
3. (~P → Q) ^ P = (P ^ ~Q) V (P ^ Q)






