Class 12 ISC- Java
Class 12th Java aims to empower students by enabling them to build their own applications introducing some effective tools to enable them to enhance their knowledge, broaden horizons, foster creativity, improve the quality of work and increase efficiency.
It also develops logical and analytical thinking so that they can easily solve interactive programs. Students learn fundamental concepts of computing using object oriented approach in one computer language with a clear idea of ethical issues involved in the field of computing
Class 12th java topics includes revision of class 11th, constructors, user-defined methods, objects and classes, library classes , etc.
Stack / Queue / D-Queue
Stack
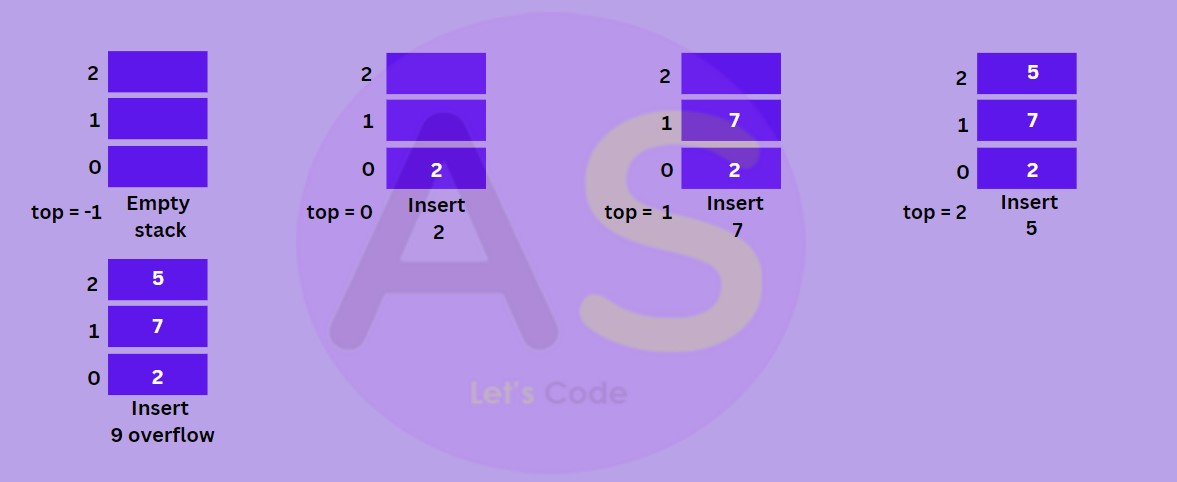
- A stack is a linear data structure any operation on stack is performed in LIFO (last in first out) order. Let us assume stack as a container so this means the element to enter the container last would be the first one to leave the container.
- An element can be pushed in the stack shown below. Any container has a limit and so does stack too. Element in a stack can only be pushed to a limit, this extra pushing of element leads to stack overflow.
Operations on Stack :
(i) In order to create a stack we need a pointer to the top most element to know about the element which is on the top so that the operation can be done on stack.
(ii) Along with that we need space for the other element to get in.
Here, are some basic operations on stack :
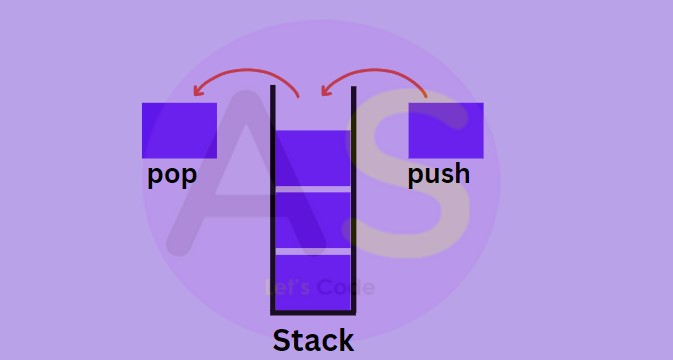
push() :
To push or insert an element in stack.
Let us see the diagram how push operation is performed
pop() :
To Pop or delete top most element from the stack.
Let us see the diagram how pop operation is performed

Underflow :
Stack underflow happens when we try to pop (remove) an element from stack when the stack is empty (i.e. top = -1)
Overflow :
Stack overflow happens when we try to push (insert) an element into stack when the stack is full (i.e. top = size - 1)
peek() :
To fetch the first element in stack or the top most element present in stack.
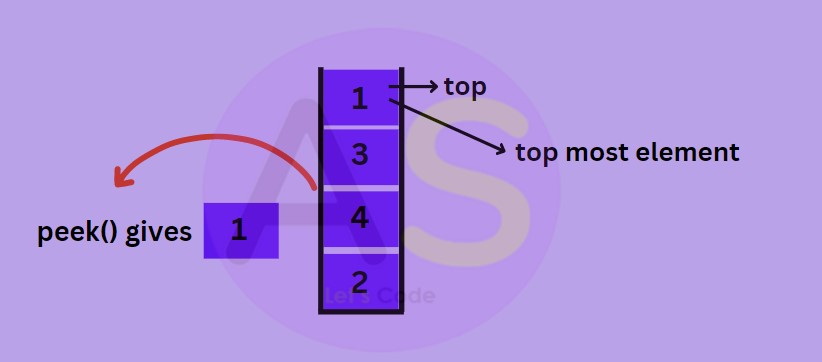
int peek ()
{
if(top==-1)
{
System.out.println("Underflow");
return -999;
}
else
{
int val = arr[top];
return val;
}
}
Program :
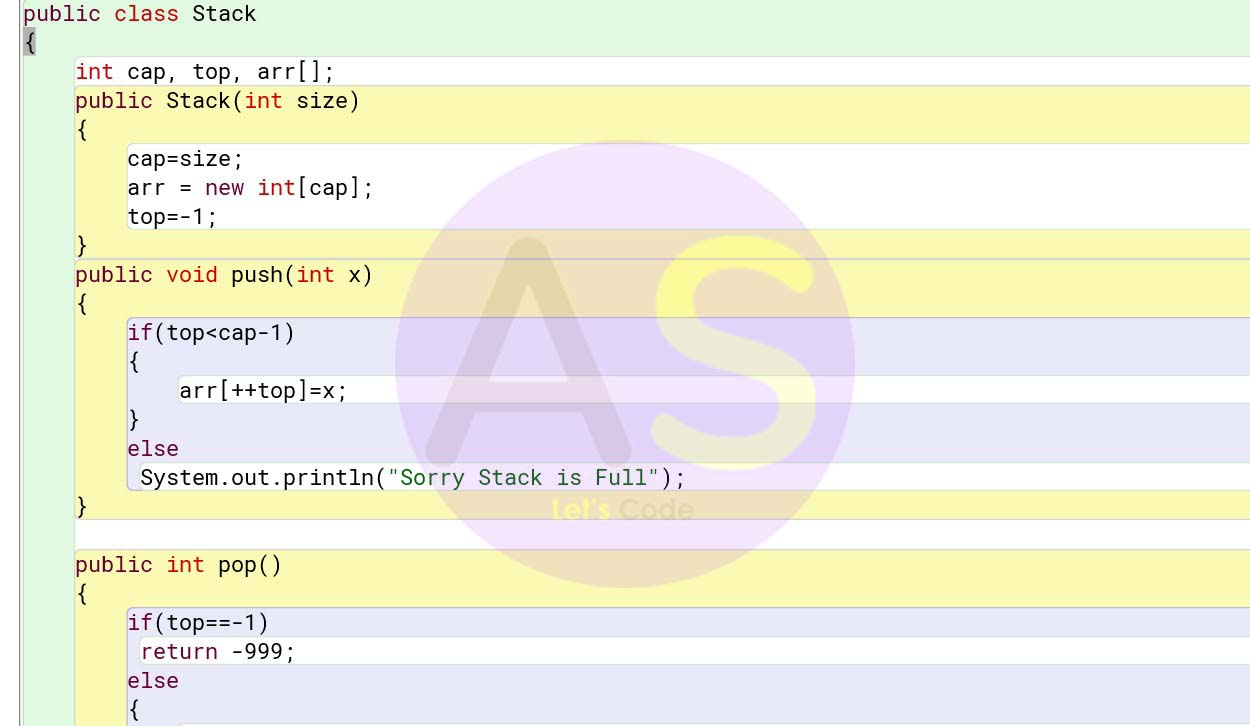

Testing Stack :
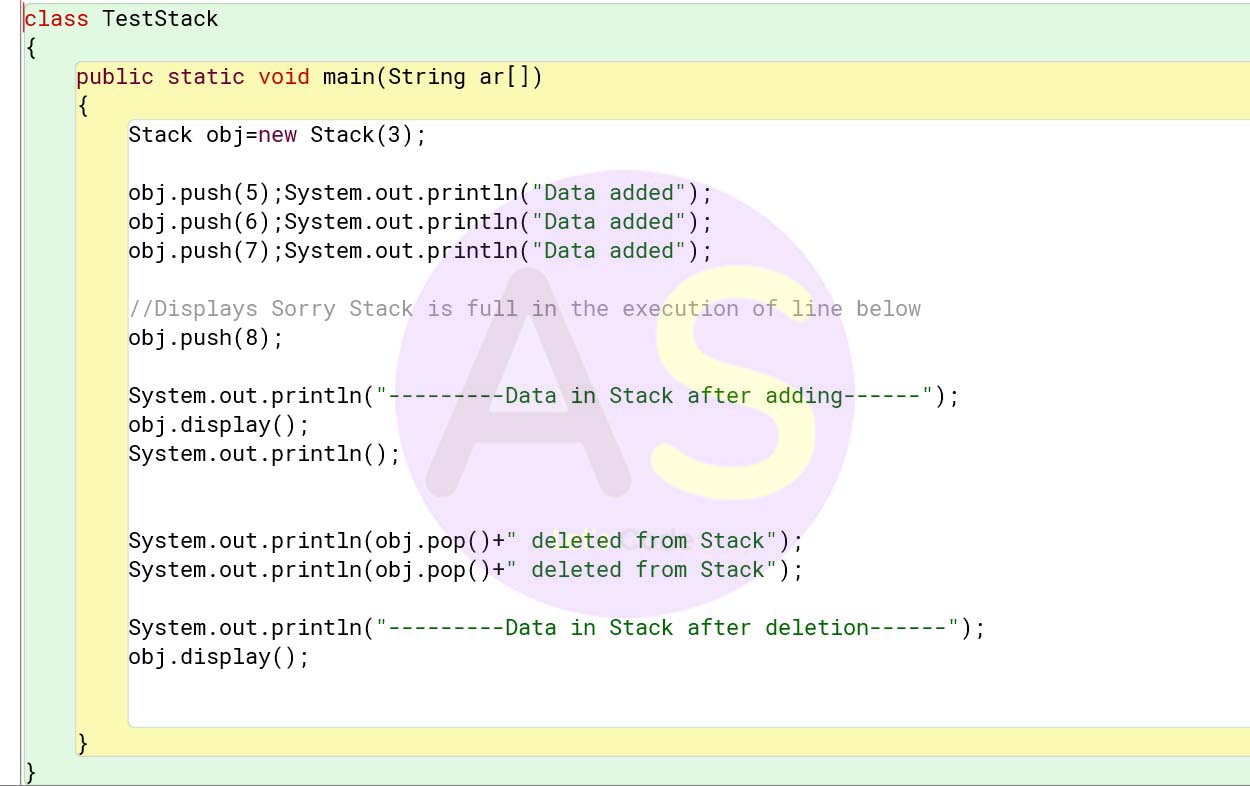
Applications of stack :
- In function calling a function until it returns reserves a space in the memory stack. Any function embedded in some function comes above the parent function , so first the embedded function will end then the parent function.
- Infix to postfix conversion.
- Parenthesis matching.
- A stack is a linear data structure any operation on stack is performed in LIFO (last in first out) order. Let us assume stack as a container so this means the element to enter the container last would be the first one to leave the container.
- An element can be pushed in the stack shown below. Any container has a limit and so does stack too. Element in a stack can only be pushed to a limit, this extra pushing of element leads to stack overflow.
(i) In order to create a stack we need a pointer to the top most element to know about the element which is on the top so that the operation can be done on stack.
(ii) Along with that we need space for the other element to get in.
Here, are some basic operations on stack :

push() :
To push or insert an element in stack. Let us see the diagram how push operation is performed

pop() :
To Pop or delete top most element from the stack. Let us see the diagram how pop operation is performed

Underflow :
Stack underflow happens when we try to pop (remove) an element from stack when the stack is empty (i.e. top = -1)
Overflow :
Stack overflow happens when we try to push (insert) an element into stack when the stack is full (i.e. top = size - 1)
peek() :
To fetch the first element in stack or the top most element present in stack.

int peek ()
{
if(top==-1)
{
System.out.println("Underflow");
return -999;
}
else
{
int val = arr[top];
return val;
}
}
Program :


Testing Stack :

Applications of stack :
- In function calling a function until it returns reserves a space in the memory stack. Any function embedded in some function comes above the parent function , so first the embedded function will end then the parent function.
- Infix to postfix conversion.
- Parenthesis matching.
peek() :
To fetch the first element in stack or the top most element present in stack.

int peek ()
{
if(top==-1)
{
System.out.println("Underflow");
return -999;
}
else
{
int val = arr[top];
return val;
}
}
Program :


Testing Stack :

Applications of stack :
- In function calling a function until it returns reserves a space in the memory stack. Any function embedded in some function comes above the parent function , so first the embedded function will end then the parent function.
- Infix to postfix conversion.
- Parenthesis matching.

int peek ()
{
if(top==-1)
{
System.out.println("Underflow");
return -999;
}
else
{
int val = arr[top];
return val;
}
}



- In function calling a function until it returns reserves a space in the memory stack. Any function embedded in some function comes above the parent function , so first the embedded function will end then the parent function.
- Infix to postfix conversion.
- Parenthesis matching.
Queue
Queue is a very well known term to us , we stand in a queue while waiting for our turn to come. Indian Railways is one of the places where people stand in queue waiting for their chance to buy tickets .
Similarly in Java queue is also a linear data structure. Any operation on queue will be performed in FIFO (first in first out) order.
Real world example of queue is shown below :

Note : In queues we have to maintain both ends for insertion at one end and deletion from the other end.
Creation of Queue :
In order to create queue we need 2 pointers one for pointing insertion (i.e. rear) to store the location where the new element will be inserted. And the other one for pointing deletion end (i.e. front) to store the location where the element will be deleted.
Operations on Queue :
Enqueue :
To insert an element in the queue (i.e. from rear end).
While inserting an element in queue. We need to :
- Check whether the queue is full (i.e. overflow situation).
- For the first element set the value of front to zero (i.e. front = 0).
- Increase the rear index by one
-
Add the new element to the position pointed by rear.
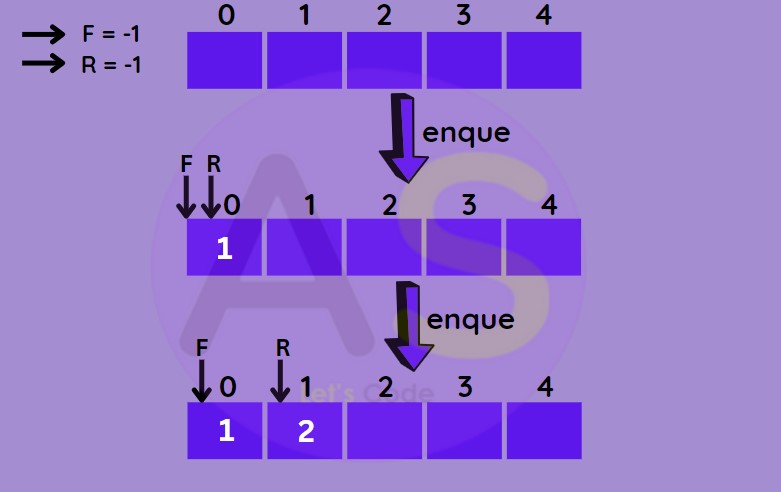
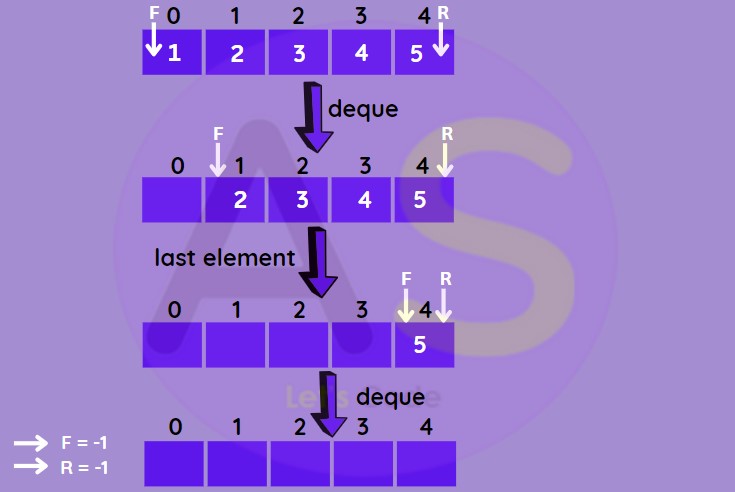
Dqueue :
To remove an element from the queue (i.e. from front end). While removing element from the queue need to :
- Check whether the queue is empty (i.e. underflow situation).
- Return the value pointed by the front.
- Increase the front by one
-
For last element reset the values of front and rear to - 1.
peek () in Queue :
It is used to check the value in queue and return the value.
public int peek()
{
if(front == -1 && rear == -1)
{
Syatem.out.println("Underflow");
return -999;
}
else if(front == rear)
{
int val = arr[front];
return val;
}
}
Program :


Testing Queue :
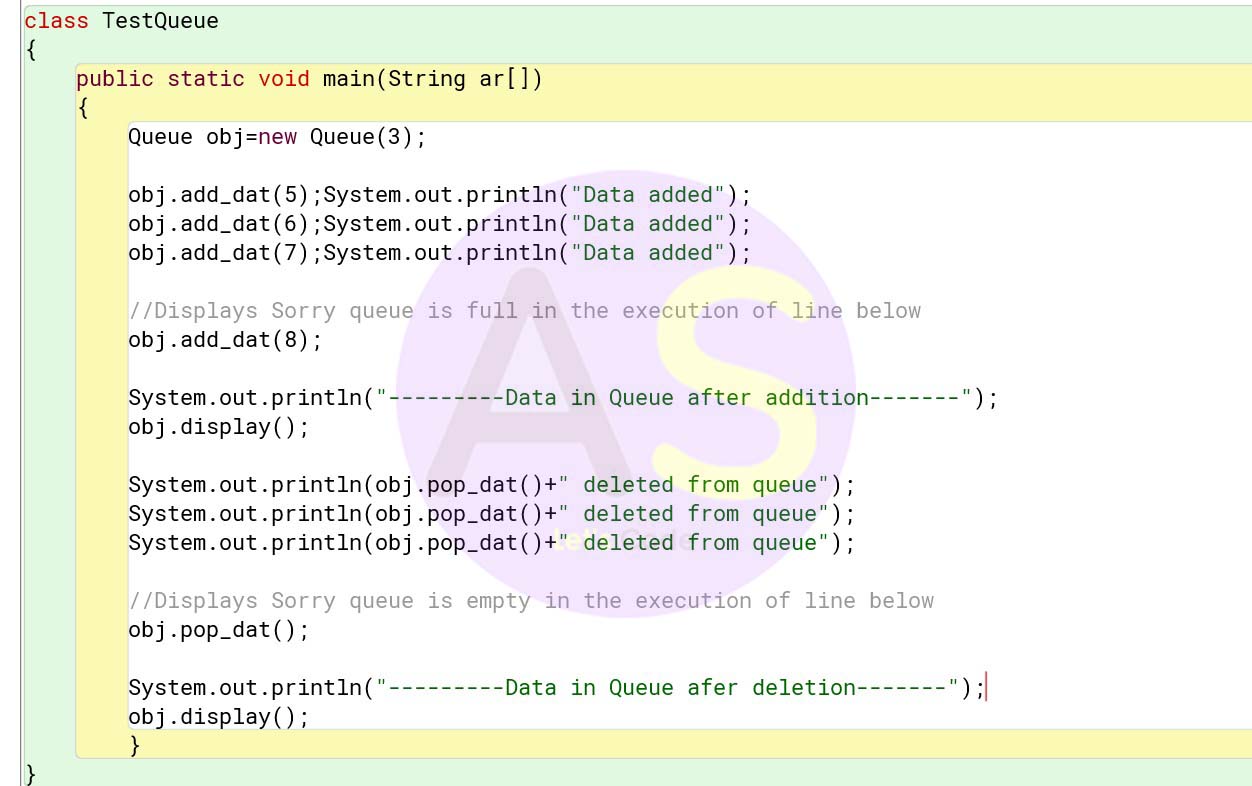
Similarly in Java queue is also a linear data structure. Any operation on queue will be performed in FIFO (first in first out) order.
Real world example of queue is shown below :

Note : In queues we have to maintain both ends for insertion at one end and deletion from the other end.
In order to create queue we need 2 pointers one for pointing insertion (i.e. rear) to store the location where the new element will be inserted. And the other one for pointing deletion end (i.e. front) to store the location where the element will be deleted.
Operations on Queue :
Enqueue :
To insert an element in the queue (i.e. from rear end). While inserting an element in queue. We need to :
- Check whether the queue is full (i.e. overflow situation).
- For the first element set the value of front to zero (i.e. front = 0).
- Increase the rear index by one
- Add the new element to the position pointed by rear.

To remove an element from the queue (i.e. from front end). While removing element from the queue need to :
- Check whether the queue is empty (i.e. underflow situation).
- Return the value pointed by the front.
- Increase the front by one
- For last element reset the values of front and rear to - 1.

It is used to check the value in queue and return the value.
public int peek()
{
if(front == -1 && rear == -1)
{
Syatem.out.println("Underflow");
return -999;
}
else if(front == rear)
{
int val = arr[front];
return val;
}
}
Program :


Testing Queue :

De-Queue
As the name suggests this variant of queue is double ended. This means unlike normal queues where insertion could only happen at the rear end, and deletion at the front end, in these double ended queues insertion and deletion of elements can happen from both the ends of their choice.
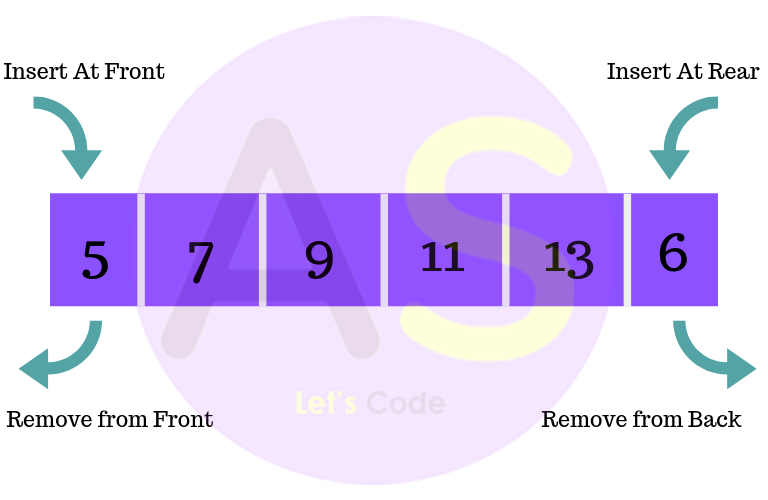
Characteristics of De-Queue
- They do not follow FIFO principle.
- Insertion can be done at both the ends of the de-queue.
- Deletion can also be done at the both ends of the de-queue.
Types of De-Queue
Input Restricted De-Queue :
In this de-queue input is restricted at a single end but allows deletion from both the ends.
Output Restricted De-Queue :
In this de-queue output is restricted at a single end but allows insertion from both the ends.
Operations in De-Queue
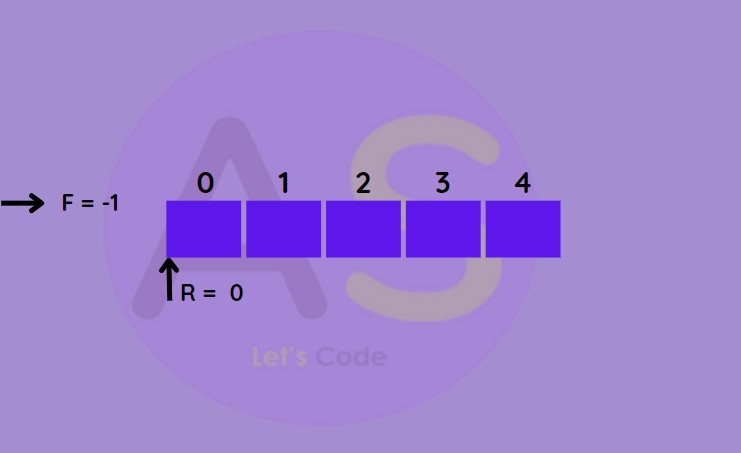
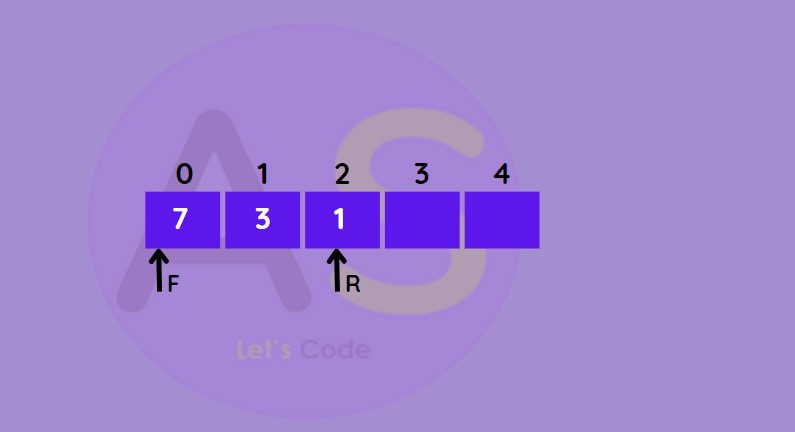
- Take a de-queue of size n
- Set two pointers at first position front = -1 and rear = 0
Insert at the front :
This operation adds an element at the front
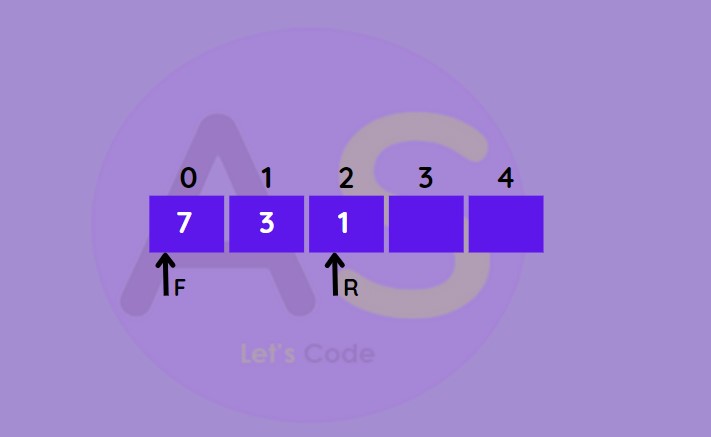
- If front < 1 then initialise it front = n -1 (last index)
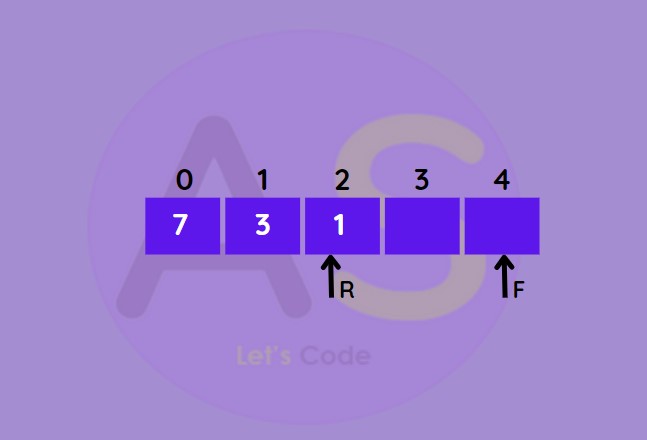
- Else decrease front by 1
- Add new element into de-queue.
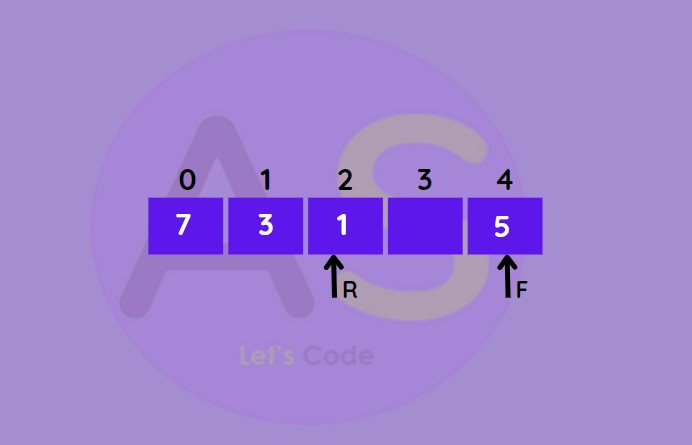
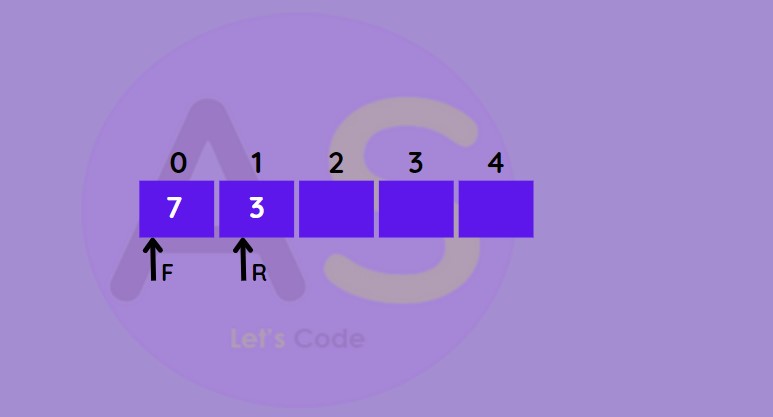
Insert at the rear :
This operation adds an element at the rear.
- Check if de-queue is full.
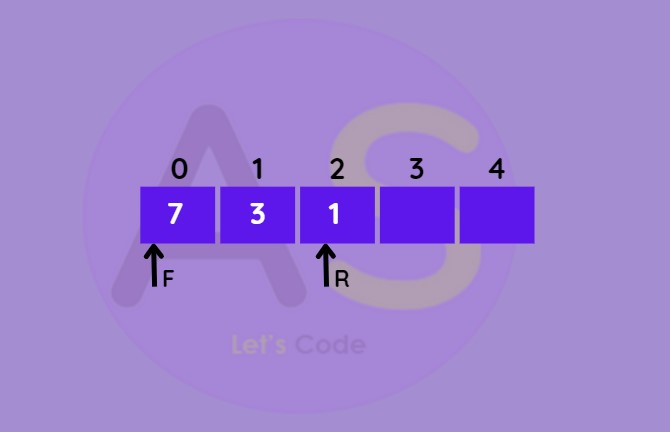
- If full then make rear = 0
- Else increase rear by 1
- Add new element into de-queue.
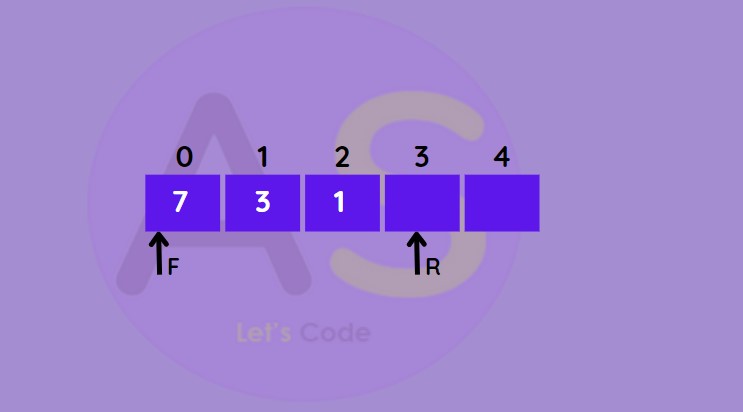
Delete from front :
This operation deletes an element from the front.
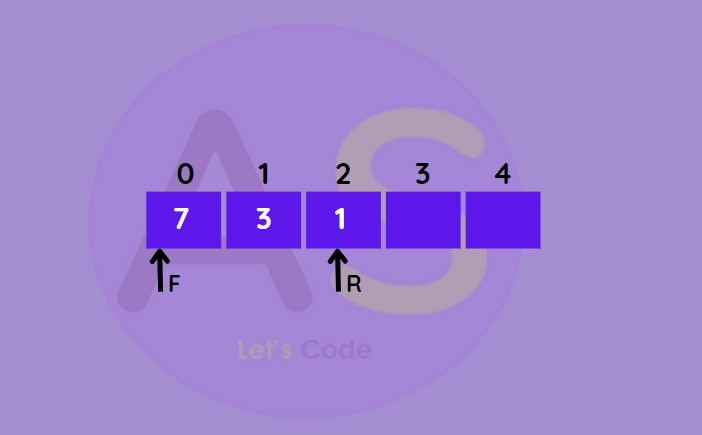
- Check if de-queue is empty.
- If empty (i.e. front = -1) underflow situation occurs.
- If not empty and has one element (i.e. front = rear) then set front and rear -1
- If front = n-1 (last index i.e. at the end) then set front = 0
- Otherwise increased front by 1
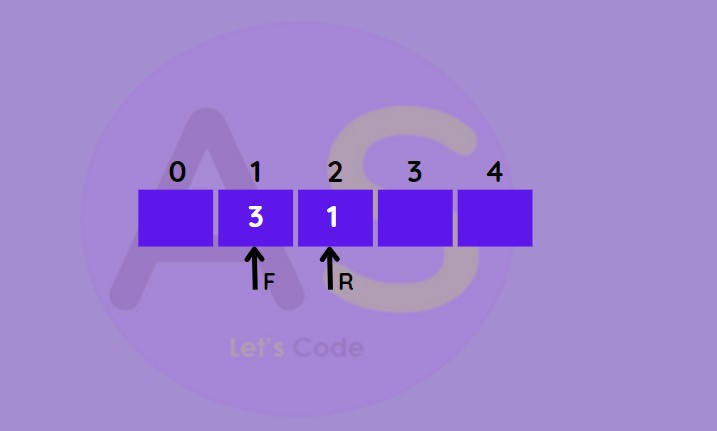
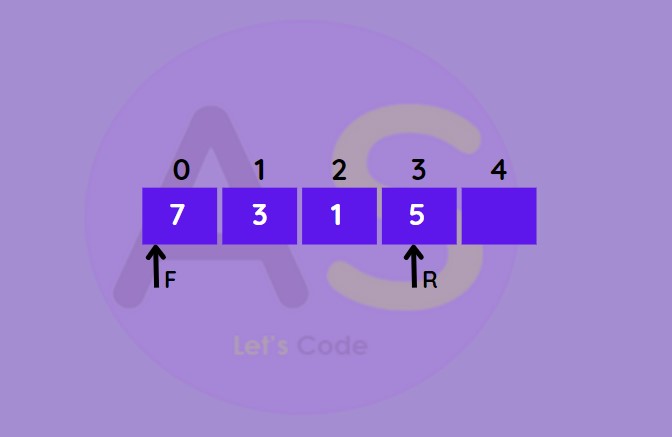
Delete from rear :
This operation deletes an element from the rear.
- Check if de-queue is empty.
- If empty (i.e. front = -1) underflow situation occurs.
- If not empty and has one element (i.e. front = rear) then set front and rear -1
- If rear = 0 then set it to as rear = n-1 (last index i.e. at the end)
- Otherwise decrease rear by 1
To check if De-queue is empty :
This operation is used to check whether de-queue is empty (i.e. front = -1 then de-queue is empty).
To check if De-queue is full :
This operation is used to check whether de-queue is full (i.e. if front = 0 and rear = n-1 or front = rear + 1 then de-queue is full)
Applications of De-Queue
- To store history in browsers.
- In undo operations on software.
- For implementing both 'stacks' and 'queues'.

Characteristics of De-Queue
- They do not follow FIFO principle.
- Insertion can be done at both the ends of the de-queue.
- Deletion can also be done at the both ends of the de-queue.
Types of De-Queue
Input Restricted De-Queue :
In this de-queue input is restricted at a single end but allows deletion from both the ends.
Output Restricted De-Queue :
In this de-queue output is restricted at a single end but allows insertion from both the ends.
Operations in De-Queue
- Take a de-queue of size n
- Set two pointers at first position front = -1 and rear = 0

Insert at the front :
This operation adds an element at the front

- If front < 1 then initialise it front = n -1 (last index)

- Else decrease front by 1
- Add new element into de-queue.

Insert at the rear :
This operation adds an element at the rear.
- Check if de-queue is full.

- If full then make rear = 0
- Else increase rear by 1

- Add new element into de-queue.

Delete from front :
This operation deletes an element from the front.

- Check if de-queue is empty.
- If empty (i.e. front = -1) underflow situation occurs.
- If not empty and has one element (i.e. front = rear) then set front and rear -1
- If front = n-1 (last index i.e. at the end) then set front = 0
- Otherwise increased front by 1

Delete from rear :
This operation deletes an element from the rear.
- Check if de-queue is empty.

- If empty (i.e. front = -1) underflow situation occurs.
- If not empty and has one element (i.e. front = rear) then set front and rear -1
- If rear = 0 then set it to as rear = n-1 (last index i.e. at the end)
- Otherwise decrease rear by 1

To check if De-queue is empty :
This operation is used to check whether de-queue is empty (i.e. front = -1 then de-queue is empty).
To check if De-queue is full :
This operation is used to check whether de-queue is full (i.e. if front = 0 and rear = n-1 or front = rear + 1 then de-queue is full)
Applications of De-Queue
- To store history in browsers.
- In undo operations on software.
- For implementing both 'stacks' and 'queues'.











- To store history in browsers.
- In undo operations on software.
- For implementing both 'stacks' and 'queues'.