Code is copied!
CLASS 12 ISC JAVA SPECIMEN PAPER 2022 Term - I
Maximum Marks: 70
Time allowed: One and a half hours
(Candidates are allowed additional 15 minutes for only reading the paper.)
ALL QUESTIONS ARE COMPULSORY
The marks intended for questions are given in brackets [ ].
Select the correct option for each of the following questions.
SECTION A
Question 1
The law which represents the Boolean equation A + B = B + A is.
- Associative Law
- Distributive Law
- Commutative Law
- Absorption Law
Solution
(c) Commutative Law
Question 2
The dual of the Boolean equation (X+Y) ·1 = X+Y is.
- X+Y + 0
- X·Y + 0 = X·Y
- (X·Y) + 1 = X·Y
- (X+Y) + 0 = X·Y
Solution
(b) X·Y + 0 = X·Y
Encapsulation
Question 3
If A=1, B=0, C=0 and D=1, then the maxterm will be.
- AB’C’D
- A’BCD’
- A+B’+C’+D
- A’+B+C+D’
Solution
(d) A’+B+C+D’
Question 4
The compliment of the Boolean expression F(P,Q,R) = (P + Q + R) is.
- P’Q’R’
- P’ + Q’ + R’
- P + (Q’+R’)
- (P+Q) + R'
Solution
(a) P’Q’R’
Question 5
The propositional operator => represents.
- Conjunction
- Implication
- Disjunction
- Negation
Solution
(b) Implication
Question 6
Encoders are used for.
- Adding two bits
- Converting Decimal to Binary
- Converting Binary to Decimal
- Data transmission
Solution
(b) Converting Decimal to Binary
Question 7
NAND gate is formed by the combinations of.
- AND gate and OR gate
- OR gate and NOT gate
- NAND gate and NOT gate
- AND gate and NOT gate
Solution
(d) AND gate and NOT gate
Question 8
The combinational circuit which adds two binary bits is.
- Full Adder
- Decoder
- Half Adder
- Multiplexer
Solution
(c) Half Adder
Question 9
The Quad group in a Karnaugh’s map eliminates.
- One variable
- Four variables
- Three Variables
- Two variables
Solution
(d) Two variables
Question 10
The proposition (a <=> b ) is represented by.
- a'b’ + ab
- (a'+b’) · (a+b)
- (a+b)’
- (a·b)’
Solution
(a) a'b’ + ab
Question 11
If the input in a decoder is A’BC’D, then the decimal equivalent output will be.
- 8
- 10
- 5
- 6
Solution
(c) 5
Question 12
A matrix MAT[10][15] is stored in the memory in Row Major Wise with each element requiring 2 bytes of storage. If the base address at MAT[1][2] is 2215, then the address of MAT[3][7] will be.
- 2285
- 2315
- 2319
- None of the above
Solution
(a)
= 2215 + 2 x (15 x (3-1) + (7-2))
= 2215 + 2 x 35
= 2215 + 70
= 2285
Question 13
With reference to the given proposition ~P => Q , answer the following questions.
-
the converse of the proposition is.
- ~Q => P
- Q => ~P
- ~Q => ~P
- ~P => ~Q
-
the contra-positive of the proposition is.
- ~P => Q
- Q => P
- ~Q => P
- ~ P => ~Q
Solution
(i) ~Q => P
Solution
(iii) ~Q => P
Question 14
The reduced expression for the Boolean expression F(X,Y,Z) = ∑(0,1,2,3,4,5,6,7) is.
- XY’ + X’Y
- 1
- 0
- None of the above
Solution
(b) 1
Question 15
What is the output of the code given below?
int i,j;
for( i=1; i<=5;i++);
for(j=i+1;j< 1;j++);
System.out.print(i + "+" + j) ;
- 67
- 1+2
- 6+7
- 12
Solution
(c)
Question 16
What is the output of the statement given below?
System.out.print(Integer.parseInt(“234”)+’A’);
System.out.print(Integer.parseInt(“234”)+’A’);
- 234+65
- 234A
- 299
- ERROR
Solution
(c)
Question 17
What is the output of the statement given below?
System.out.print(‘A’+’1’+’C’);
- 65+1+66
- 10+1+67
- 181
- 65+49+67
Solution
(c)
Question 18
The basic logic gate that represents the simplification of the Boolean expression A.(A’+B). (A+B) is.
- OR gate
- NOT gate
- AND gate
- None of the above
Solution
(c)
Question 19
What is the conditional statement to check for the Non-boundary elements in a double dimensional array of ‘M’ number of rows and ‘N’ number of columns? The row index is represented by ‘r’ and the column index is represented by ‘c’.
- (r>0 || r< M-1 && c>0 || c< N-1)
- (r>0 && r< M-1 || c>0 && c< N-1)
- (r>0 && r< M-1 && c>0 && c< N-1)
- (r>0 || r< M-1 || c>0 || c< N-1)
Solution
(b)
Question 20
The proposition ~( a ∧ b ) V (~a => b) is a.
- Contradiction
- Contingency
- Tautology
- Implication
Solution
(c)
Question 21
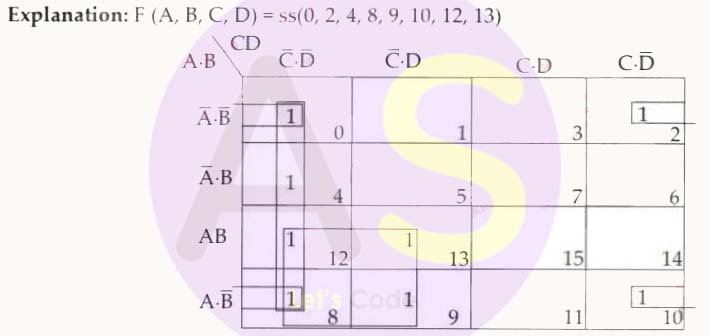
Reduce the given Boolean function F(A,B,C,D) = ∑(0,2,4,8,9,10,12,13) by using 4-variable Karnaugh map and answer the following questions.
-
What will be the least number of groups and their types formed for reduction?
- 6 pairs
- 2 quad and 2 pairs
- 1 quad and 3 pair
- 3 quads
-
The reduced expression of the Boolean function given above is:
- ACD’ + B’D’ + BD
- (A+C’+D’).(B’+D’).(A+C’)
- C’D’ + AC’ + B’D’
- (C+D’). (B’+D’).(A+B+D)
Solution
(iv)
Solution
(iii)
Question 22
A school intends to select candidates for an Inter school competition as per the criteria
given below:
-
The student has participated in an earlier competition and is very creative
OR
-
The student is very creative and has excellent general awareness, but has not
participated in any competition earlier
OR
- The student has excellent general awareness and has won prize in an inter -house
competition
The inputs are:
A - Participated in a competition earlier
B - Is very creative
C - Won prize in an inter house competition
D - Has excellent general awareness
( In all the above cases 1 indicates yes and 0 indicates no).
Output: X [ 1 indicates yes and 0 indicates no for all cases].
Draw the truth table for the inputs and outputs given above and answer the following
questions:
OR
OR
Draw the truth table for the inputs and outputs given above and answer the following questions:
-
The POS expression for X(A,B,C,D) will be:
- F(A,B,C,D) = ∑ (3, 5, 7, 11, 12, 13, 14, 15)
- F(A,B,C,D) = π (3, 5, 7, 11, 12, 13, 14, 15)
- F(A,B,C,D) = π (0, 1, 2, 4, 6, 8, 9, 10)
- F(A,B,C,D) = ∑ (0, 1, 2, 4, 6, 8, 9, 10)
-
The maximum input combinations for the above truth table will be:
- 24
- 16
- 8
- 4
Solution
(iii)
Solution
(ii) As there are 4 inputs so there will be 24 = 16 input combinations.
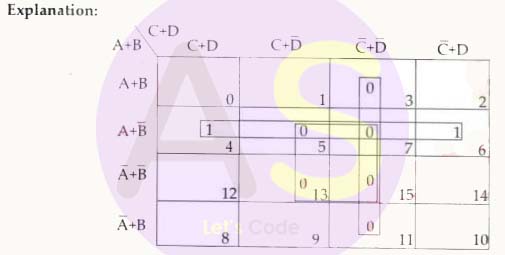
Question 23
Reduce the given Boolean function F(A,B,C,D) = π(3,4,5, 6, 7, 11,13,15) by using 4-variable Karnaugh map and answer the following questions.
-
What will be the least number of groups and their types formed for reduction?
- 6 pairs
- 3 quads
- 1 quad and 3 pairs
- 2 quad and 3 pairs
-
The reduced expression of the Boolean function given above is:
- (B+C).(B+D).(A’+D)
- BC + BD + A’D
- AB’ + C’D’ + B’D’
- (A+B’).(C’+D’).(B’+D’)
Solution
(ii) 3 quads
Solution
(iv) (A+B’).(C’+D’).(B’+D’)
Question 24
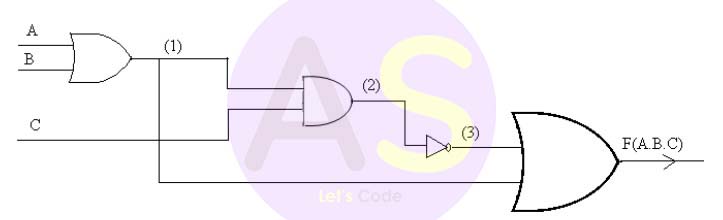
From the logic diagram given above, where A,B and C are inputs and F is the output,
answer the following questions:
-
The expression at (1) is:
- A.B
- A’+B’
- A+B’
- A+B
-
The expression at (3) is:
- A+B.C’
- ((A+B)’.C)’
- ((A+B).C)’
- (A+B).C
-
The final expression F(A,B,C) is:
- F=((A+B)’.C)’ + (A+B)
- F=((A+B)’.C)’ + (A+B)
- F=( (A+B).C)’ + (A+B)
- F= (AB + C)’ +(A+B)
Solution
(iv) A+B
Solution
(iii) ((A+B).C)’
Solution
(iii) F=( (A+B).C)’ + (A+B)
Question 25
Given the Boolean expression F = ( P + R) · ( P·Q + Q·R’ ), identify:
-
The complement of the expression:
- P’R’ + (P’+Q’).(Q’+R)
- (P’+R’) . (P’+Q’) + (Q+R’)
- P’R’ .(PQ’ + Q’R)
- (P+R)’ .(P’+Q).(Q’+R)
-
The law used:
- Distributive Law
- De Morgan Law
- Associative Law
- Idempotent Law
Solution
(i)
Explanation:
Applying the DeMorgan's law
F ( P + R) ( PQ + QR. )
= ((P+R). (P.Q + Q•R'))'
= ((P+R)' + (P.Q +Q.R')') (De-morgan's law)
= P'. R' + (P'+Q')(Q'+R)
Solution
(ii)
Question 26
With reference to the program code given below, answer the questions that follow:
void fun(int n)
{ int i,f;
for( i=1,f=1;i<=n;i++,f*=i);
System.out.print(f);
}
-
What is the output of the method fun() when the value of n=4?
- 24
- 72
- 120
- ERROR
-
What is the method fun() performing?
- Checking for Prime Numbers
- Product of odd numbers
- Factors of a number
- Finding the factorial
Solution
(ii)
Solution
(iv)
Question 27
With reference to the program code given below, answer the questions that follow:
int test(int n)
{ if(n==1) return 0;
for (int i=2;i<=(int)(Math.sqrt(n));i++)
if( n%i==0)
return 0;
return 1;
}
-
What will the method test() return when the value of n=9?
- 1
- true
- 0
- Error
-
What is the method test() performing?
- Prime number/Composite number
- Armstrong number
- Palindrome number
- Perfect number
Solution
(iii)
Solution
(i)
Question 28
With reference to the program code given below, answer the questions that follow:
void dimen(int n[ ][ ])
{ int p=0;
for (int i=0;i< n.length;i++)
for(int j=0;j< n[0].length;j++)
{ if(i==0 ||i==n.length-1 || j==0 || j==n[0].length-1)
p=p+n[i][j];
}
System.out.print(p);
}
-
What will be the output of the method dimen() when the value of
n[ ][ ] ={{2,3,7},{1,5,9},{10,-3,8}} ?
- 42
- 33
- 5
- 37
-
What is the method dimen( ) performing?
- Finding the product of the boundary elements
- Finding the sum of the non-boundary elements
- Finding the sum of the boundary elements
- Finding the sum of the matrix elements
Solution
(iv)
Solution
(iii)
Question 29
With reference to the program code given below, answer the questions that follow:
void single(int x[])
{ int w=1;
for(int y=0;y< x.length;y++)
{ if(x[y]%2==0 && x[y]>0)
w=w*x[y];
}
System.out.print(w);
}
-
What will be the output of the method single() when the value of
x[] = {10,2,9,-6,5,6} ?
- 120
- 45
- 720
- 18
-
What is the method single( ) performing?
- Sum of the positive odd elements
- Product of the even elements
- Product of the positive even elements
- Sum of the positive even elements
Solution
(i)
Solution
(iii)
Question 30
With reference to the program code given below, answer the questions that follow:
int solve(int a, int b)
{ int i,l=0;
for(i=1;i<=a*b;i++)
{ if(i%a==0&& i%b==0)
{ l=i; break;}
}
return l;
}
-
What will be the output of the method solve() when the value of a=8 and b=12?
- 4
- 96
- 0
- 24
-
What is the method solve( ) performing?
- HCF of ‘a’ and ‘b’
- Prime Factors of ‘a’ and ‘b’
- LCM of ‘a’ and ‘b’
- None of the above
Solution
(iv)
Solution
(iii)
Question 31
The following program code checks if the positive integer ‘N’ is a palindrome number
by returning true or false. There are some places in the code marked as ?1?, ?2?, ?3?,
?4? and ?5? which are to be replaced by a statement/expression so that the code works
properly.
boolean Palindrome(int N)
{ int rev = ?1? ;
int num = N;
while (num>0)
{ int f = num/10;
int s = ?2? ;
int digit = num − ?3? ;
rev = ?4? + digit;
num /= ?5?;
}
if(rev == N)
return true;
else
return false;
}
Answer the following question:
-
What is the statement or expression at ?1?
- -1
- 0
- 10
- 2
-
What is the statement or expression at ?2?
- s *10
- f /10
- rev
- f *10
-
What is the statement or expression at ?3?
- s
- rev
- f
- digit * 10
-
What is the statement or expression at ?4?
- s * 10
- rev *10
- f
- rev
-
What is the statement or expression at ?5?
- 1
- 100
- 10
- rev
Solution
(ii)
Solution
(iv)
Solution
(i)
Solution
(ii)
Solution
(iii)
Question 32
The following program code sorts a single dimensional array in ascending order using
Insertion Sort technique. There are some places in the code marked as ?1?, ?2?,
?3?, ?4? and ?5? which are to be replaced by a statement/expression so that the code
works properly.
void insertionSort(int array[])
{ int n = ?1?;
for (int j = 1; j < n; j++)
{
int key = ?2?;
int i = j-1;
while ( (i > -1) && ( array [i] > ?3? ) )
{
array [i+1] = ?4?;
i--;
}
?5? = key;
}
Answer the following question
-
What is the statement or expression at ?1?
- array.length()
- array.length
- length
- -1
-
What is the statement or expression at ?2?
- j
- array[j+1]
- array[j]
- 0
-
What is the statement or expression at ?3?
- key
- array[j]
- i+1
- n
-
What is the statement or expression at ?4?
- j+1
- key
- array[j]
- array[i]
-
What is the statement or expression at ?5?
- array[i+1]
- i+1
- j
- array[i]
Solution
(ii)
Solution
(iii)
Solution
(i)
Solution
(iv)
Solution
(i)
Contact Us
REACH US
SERVICES
- CODING
- ON-LINE PREPARATION
- JAVA & PYTHON
ADDRESS
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+ 919839520987
Email:info@alexsir.com