Class 12 ISC - Java Question Paper 2019



PART I

(Attempt all questions)


Question 1

(a) Name and draw the logic gate represented by the following truth table, where A and B are inputs and X is the output.


Solution

(a) XOR gate


(b) Write the canonical POS expression of: F(P, Q) = Π(0, 2)

Solution

(b) (A + B).(A’ + B)

(c) Find the dual of: X.Y+X.Y’ = X + 0

Solution

(c) (X + Y).(X + Y’) = X.1

(d) If F(A, B, C) = A’.B’.C’ + A’.B.C’ then find F’ using De Morgan’s Law.

Solution

(d) (AB’C + ABC’) (∵ x’ + y’ = x’.y’)
= (AB’C’)’. (A’.B.C’)’ (∵(x’.y’) = x’ + y’)
= ((A’B’)’ + (C)’. ((A’B)’ + (C’)’)
= ((A’)’ + (B’)’) + C).((A’)’ + (B)’ + C)
= (A + B + C).(A + B’ + C)
= AA + AB’ + AC + BA + BB’ + BC + CA + CB’ + CC (∵x.x = x)
= A + AB’ + C + AC + AB + B’C + BC

(e) If A = “It is cloudy” and B = “It is raining”, then write the proposition for
(i) Contrapositive
(ii) Converse

Solution

(e) (i) If it is not raining then it is not cloudy.
(ii) If it is raining then it is cloudy
Question 2

(a) What is an Interface? How is it different from a class?

Solution

(a) An interface is just like Java Class, but it only has static constants and abstract method. Java uses Interface to implement multiple inheritances. An interface is syntactically similar to a class, but it lacks in field declaration and the methods inside an interface do not have any implementation. A class can be instantiated but an interface not.

(b) A matrix ARR[-4 ….. 6, 3 ……. 8] is stored in the memory with each element requiring 4 bytes of storage. If the base address is 1430, find the address of ARR[3] [6] when the matrix is stored in Row Major Wise.

Solution

(b) Given, Address of ARR[3] [6] = 1430
According to row-major,
Address = B + w(n(p – L1) + (q – L2)
B = 1430, w = 4 bytes
p = 3, q = 6,U1 = 6, U2 = 8, L1 = -4, L2 = 3
Number of columns n = U2 – L2 + 1
⇒ n = 8 – 3 + 1 = 6
Address of ARR[3][6] = 1430 + 4(6 (3 – (-4))+ (6 – 3))
= 1430 + 4(6 × 7 + 3)
= 1430 + 180
= 1610

(c) Convert the following infix notation to postfix form:
(A + B * C) – (E * F / H) + J

Solution

(c) (A + B * C) – (E * F / H) + J
= (A + (BC*)) – ((EF*) / H) + J
= (ABC *+) – (EF * H/) + J
= (ABC *+ EF * H/-) + J
= ABC*+ EF * H / – J*

(d) Compare the two complexities O(n2) and O(2n) and state which is better and why.

Solution

(d) O(n2) is better than O(2n)
Let us see with the help of an example.
Suppose n = 8
n2 = 82 = 64
2n = 28 = 256
Therefore, the complexity in 2n is higher than n2. If n increases, 2n increases much more than n2. Therefore, the time complexity is O(n2) is better than O(2n).

(e) State the difference between internal nodes and external nodes of a binary tree structure.

Solution

(e) Internal nodes are not leaf nodes whereas external nodes are leaf nodes.
Question 3
The following function Mystery( ) is a part of some class. What will the function Mystery( ) return when the value of num=43629, x=3 and y=4 respectively? Show the dry run/working.
int Mystery (int num, int x, int y)
{
if(num < 10)
return num;
else
{
int z = num % 10;
if(z%2 == 0)
return z*x + Mystery (num/10, x, y);
else
return z*y + Mystery(num/10, x, y);
}
}

Solution

Given n = 43629, x = 3, y = 4
Step 5 returns 4
Step 4 returns 12 + 4 = 16
Step 3 returns 18 + 16 = 34
Step 2 returns 6 + 34 = 40
Step 1 returns 36 + 40 = 76


PART II



SECTION A

(Attempt any two questions from this Section.)


Question 4

(a) Given the Boolean function F(A, B, C, D) = Σ (0, 2, 3, 4, 5, 8, 10, 11, 12, 13).
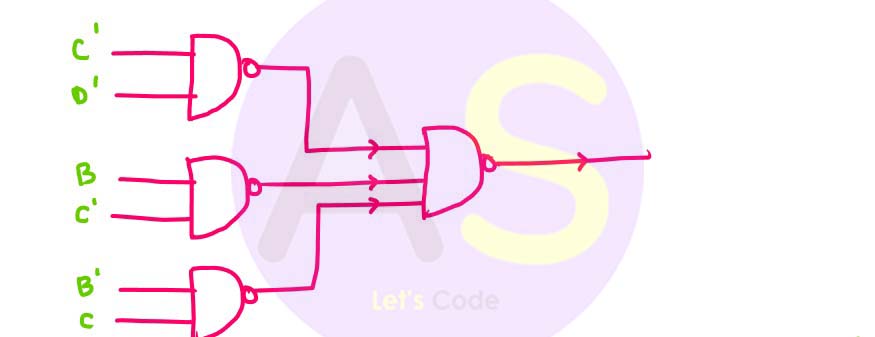
(i) Reduce the above expression by using 4-variable Karnaugh map, showing the various groups (i.e. octal, quads and pairs).
(ii) Draw the logic gate diagram for the reduced expression using only NAND gates. Assume that the variables and their complements are available as inputs.
(b) Given the Boolean function : F(P, Q, R, S) = π (0, 1, 2, 8, 9, 11, 13, 15).
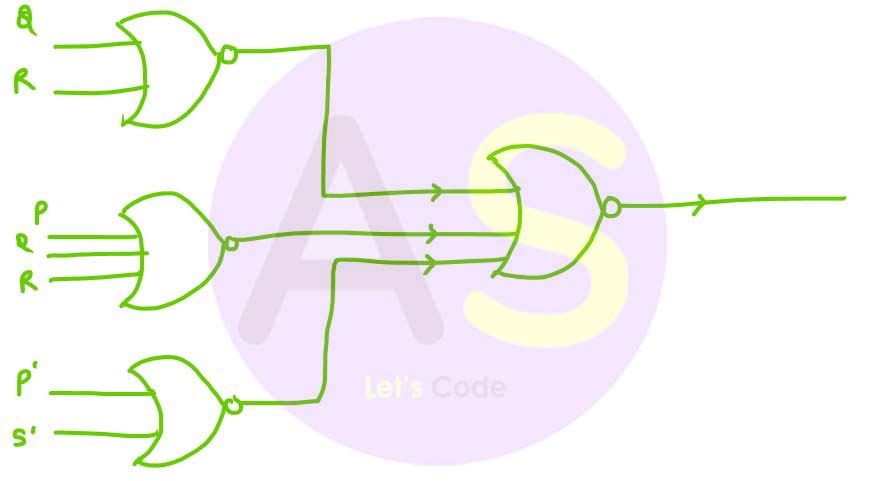
(i) Reduce the above expression by using a 4-variable Karnaugh map, showing the various groups (i.e, octal, quads and pairs).
(ii) Draw the logic gate diagram for the reduced expression using only NOR gates. Assume that the variables and their complements are available as inputs.

Solution

(a) (i)



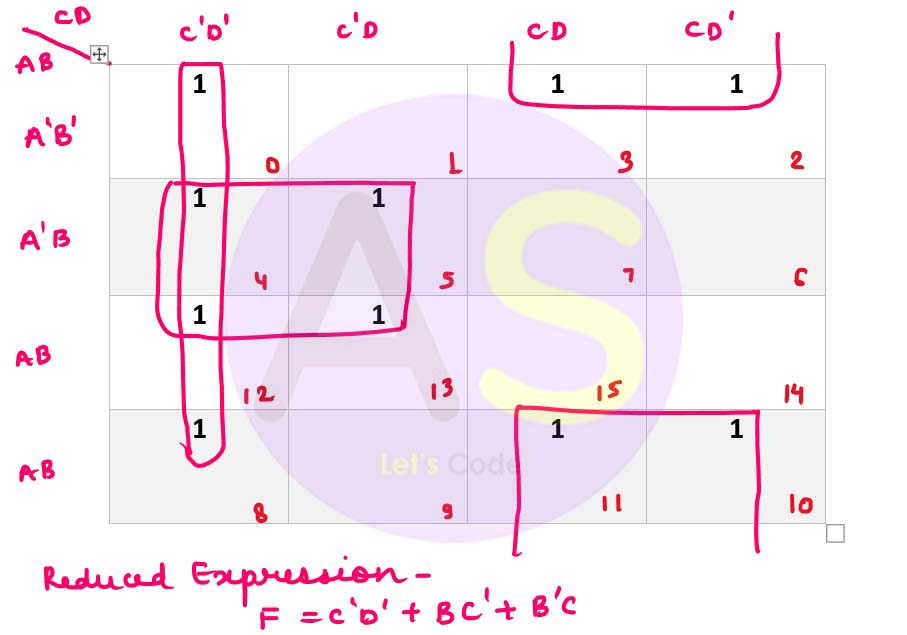
(ii)



(b) (i)



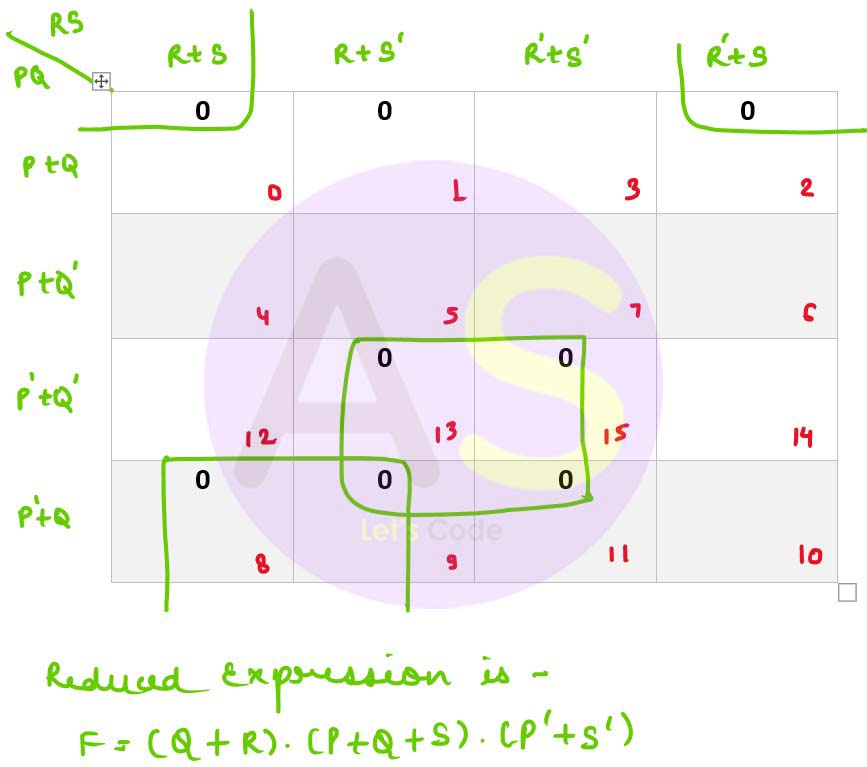
(ii)



Question 5

(a) How is a decoder different from a multiplexer? Write the truth table and draw the logic circuit diagram for a 3 to 8 decoder and explain its working.
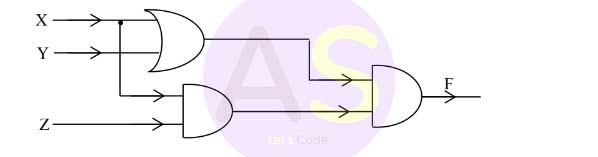
(b) From the logic circuit diagram given below, derive the Boolean expression and simplify it to show that it represents a logic gate. Name and draw the logic gate.

(c) Using a truth table, state whether the following proposition is a Tautology, Contradiction or Contingency:
~(P =>Q)<=>(~P∨Q)

Solution

(a) A multiplexer is a device which consists of multiple input channels through a single line while decoder consists of multiple inputs passing through multiple outputs. Multiplexer converts inputs from unary codes (initial) to binary codes while decoder converts binary codes to inputs.




(b)

Expression : F = (X+Y). XZ
= XZ +XYZ
= XZ
It represents AND gate.



(c)


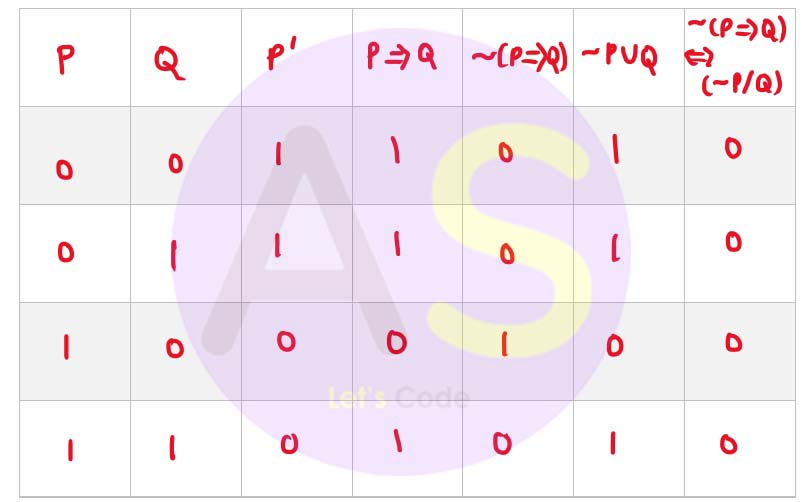
The proposition is a contradiction
Question 6

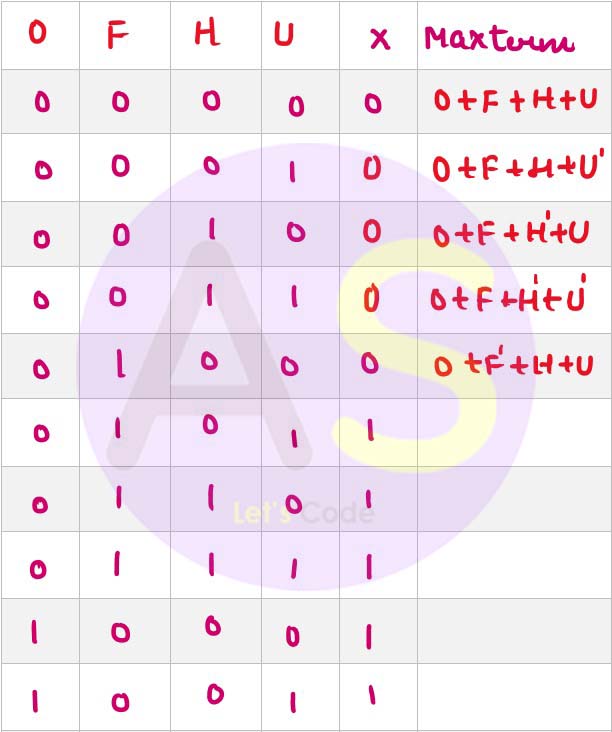
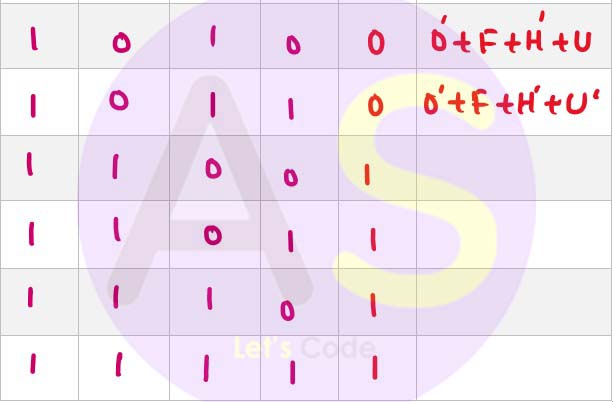
(a) The owner of a company pays the bonus to his salesmen as per the criteria are given below:
If the salesman works overtime for more than 4 hours but does not work on off days/ holidays.
OR
If the salesman works when festival sales are on and updates showroom arrangements.
OR
If the salesman works on an off day/holiday when the festival sales are on.
The inputs are O - Works overtime for more than 4 hours
F - Festival sales are on
H - Working on an off day/holiday
U - Updates showroom arrangements
(In all the above cases 1 indicates yes and 0 indicates no)
Output: X[1 indicates yes, 0 indicates no for all cases]
Draw the truth table for the inputs and outputs given above and write the POS expression for X(O, F, H, U).
(b) What is a half adder? Write the truth table and derive an SOP expression for sum and carry for a half adder.
(c) Simplify the following expression, using Boolean laws:
(X + Z).(X.Y + Y.Z’) + X.Z + Y

Solution

(a)




(b) The half adder is an example of a simple, functional digital circuit built from two logic gates. The half adder adds two one-bit binary numbers (AB). The output is the sum of the two bits (S) and the carry (C). The truth table for a half-adder is:





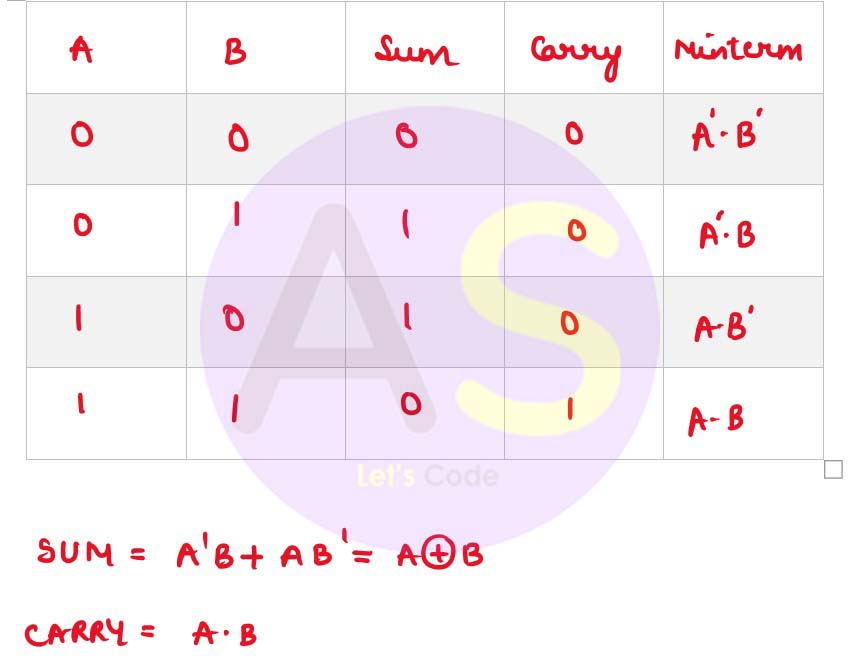
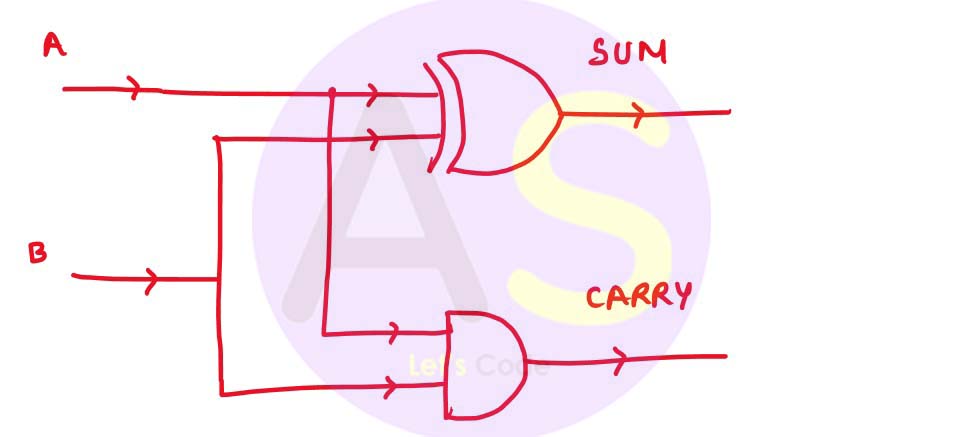
The simplified sum of products (SOP) expressions is:
S = x’y + xy’, C = xy

(c) (X + Z).(X.Y + Y.Z’) + X.Z + Y
= (X + Z).(Y.Z’) + X.Z + Y (a.b = 0)
= X.Y.Z’ + Z.Z’ + X.Z + Y (a.a’ = 0) and (a.c = 0)
= 0.Z’ + 0 + 0 + Y
= Y


SECTION B

(Attempt all questions from this Section.)


Question 7 

Design a class ArmNum to check if a given number is an Armstrong number or not.
 [A number is said to be Armstrong if sum of its digits raised to the power of length of the number is equal to the number]

Example:

371 = 33 + 73 + 13
1634 = 14 + 64 + 34 + 44
54748 = 55 + 45 + 75 + 45 + 85

Thus, 371, 1634 and 54748 are all examples of Armstrong numbers.

Some of the members of the class are given below:

Class name: ArmNum

Data members/instance variables:

n: to store the number
l: to store the length of the number

Methods/Member functions:

ArmNum (int nn): parameterized constructor to initialize the data member n = nn

int sum_pow(int i): returns the sum of each digit raised to the power of the length of the number using recursive technique eg., 34 will return 32 + 42 (as the length of the number is 2)

void isArmstrong(): checks whether the given number is an Armstrong number by invoking the function sum_pow () and displays the result with an appropriate message.

Specify the class ArmNum giving details of the constructor( ), int sum_pow(int) and void isArmstrong( ). Define a main() function to create an object and call the functions accordingly to enable the task.
Solution:


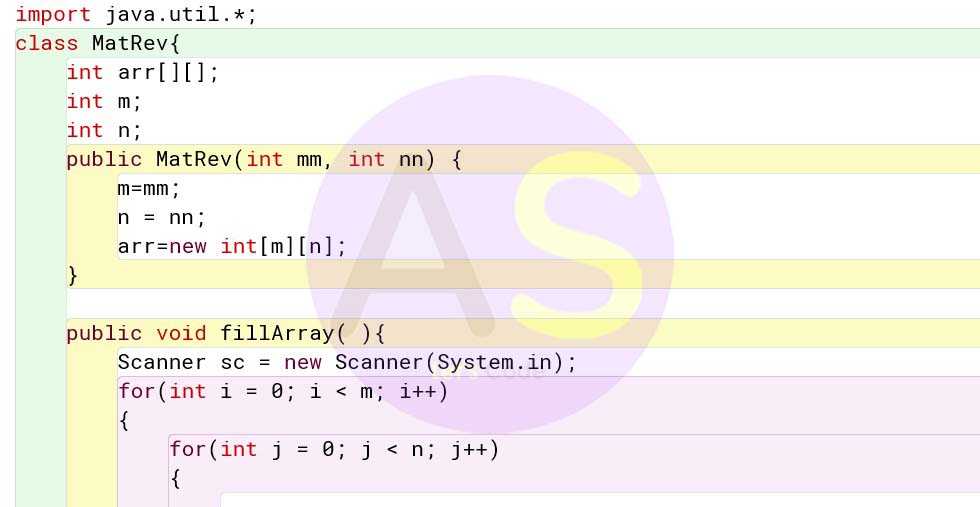
import java.util.*;
class ArmNum
{
    int n;
    int l;
    ArmNum(int nn)
    {
        n=nn;
        l=0;
    }
    
    int sum_pow(int i)
    {
        if(i!=0)
        {
            return (int)Math.pow(i%10,l)+sum_pow(i/10);
        }
        else
        {
            return 0;
        }
    }
    void isArmstrong()
    {
        int n1=n;
        while(n1!=0)
        {
            ++l;
            n1=n1/10;
        }
        
        int sum=sum_pow(n);
        if (sum==n)
        {
            System.out.println("Armstrong no.");
        }
        else
        {
            System.out.println("Not an Armstrong no.");
        }
        }
    public static void main(String args[])
    {
        Scanner sc=new Scanner(System.in);
        System.out.println("Enter a number:");
        int no=sc.nextInt();
        ArmNum obj=new ArmNum(no);
        obj.isArmstrong();
    }
    }



Question 8 

Design a class MatRev to reverse each element of a matrix. 
Example:



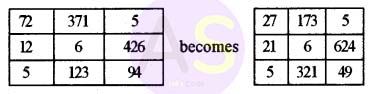Some of the members of the class are given below:

Class name: MatRev

Data members/instance variables:

arr[][] : to store integer elements
m: to store the number of rows
n: to store the number of columns

Member functions/methods:

MatRev(int mm, int nn): parameterized constructor to initialise the data members m = mm and n = nn

void fillarray(): to enter elements in the array

int reverse(int x): returns the reverse of the number x

void revMat(MatRev P): reverses each element of the array of the parameterized object and stores it in the array of the current object

void show(): displays the array elements in matrix form

Define the class MatRev giving details of the constructor ( ), void fillarray (), int reverse(int), void revMat(MatRev) and void show(). Define the main () function to create objects and call the functions accordingly to enable the task.
Solution:


import java.util.*;
class MatRev{
    int arr[][];
    int m;
    int n;
    public MatRev(int mm, int nn) {
        m=mm;
        n = nn;
        arr=new int[m][n];
    }

    public void fillArray( ){
        Scanner sc = new Scanner(System.in);

        for(int i = 0; i < m; i++) 
        {
            for(int j = 0; j < n; j++) 
            {
                System.out.println("Enter the "+i+j+" Element: ");
                arr[i][j] = sc.nextInt();
            }
        }
    }

    public int reverse(int x) 
    {
        int r = 0;
        while(x> 0)
        {
            r=r* 10+x % 10;
            x =x/ 10;
        }
        return r;
    }

    public void revMat(MatRev P) 
    {
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++) 
            {
                this.arr[i] [j] = reverse(P.arr[i] [j]);
            }
        }
    }

    public void show() {
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                System.out.print(arr[i][j] + "\t");
            }
            System.out.println();
        }
    }

    public static void main(String args[])
    {
        Scanner sc = new Scanner(System.in);
        System.out.print("Enter number of rows::");
        int x = sc.nextInt();
        System.out.print("Enter number of columns::");
        int y = sc.nextInt();
        MatRev obj1 = new MatRev(x, y);
        MatRev obj2 = new MatRev(x, y);
        obj1.fillArray();
        obj2.revMat(obj1);
        System.out.println("Original Matrix is::");
        obj1.show();
        System.out.println("Matrix with reversed elements");
        obj2.show();
    }
}



Question 9 

A class Rearrange has been defined to modify a word by bringing all the vowels in the word at the beginning followed by the consonants.

Example:

ORIGINAL becomes OIIARGNL

Some of the members of the class are given below:

Class name: Rearrange

Data Member/instance variable:

wrd: to store a word
newwrd: to store the rearranged word

Member functions/methods:

Rearrange(): default constructor

void readword(): to accept the word in UPPER case

vow freq_vow_con(): finds the frequency of vowels and consonants in the word and displays them with an appropriate message

void arrange(): rearranges the word by bringing the vowels at the beginning followed by consonants

void display(): displays the original word along with the rearranged word

Specify the class Rearrange, giving the details of the constructor(), void readword(), void freq _vow_con(), void arrange() and void display(). Define the main() function to create an object and call the functions accordingly to enable the task.
Solution:



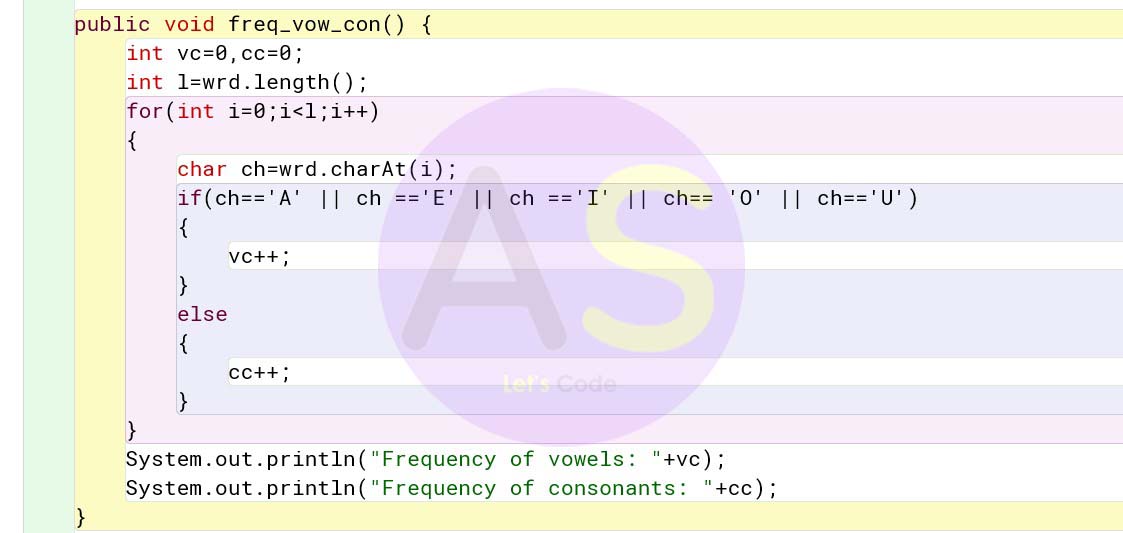
import java.util.*;
class Rearrange {
    String wrd;
    String newwrd;
    public Rearrange() {
        wrd = "";
        newwrd = "";
    }

    public void readword(){
        Scanner sc = new Scanner(System.in);
        System.out.print("Enter the word in Upper Case:");
        wrd = sc.next();
    }

    public void freq_vow_con() {
        int vc=0,cc=0;
        int l=wrd.length();
        for(int i=0;i< l;i++)
        {
            char ch=wrd.charAt(i);
            if(ch=='A' || ch =='E' || ch =='I' || ch== 'O' || ch=='U')
            {
                vc++;
            }
            else
            {
                cc++;
            }
        }
        System.out.println("Frequency of vowels: "+vc);
        System.out.println("Frequency of consonants: "+cc);
    }

    public void arrange() {
        String v ="";
        String c = "";
        for(int i = 0; i < wrd. length(); i++) {
            char ch = wrd.charAt(i);
            if(ch=='A' || ch =='E' || ch =='I' || ch== 'O' || ch=='U')
            {
                v+=ch;
            }
            else
            {
                c+=ch;
            }

        }
        newwrd = v + c;
    }

    public void display() {
        System.out.println("Original word:" + wrd);
        System.out.println("Rearranged word:" + newwrd);
    }

    public static void main(String args[]) {
        Rearrange obj = new Rearrange();
        obj.readword();
        obj.freq_vow_con();
        obj.arrange();
        obj.display();
}
}



Question 10 

A superclass Record contains names and marks of the students in two different single dimensional arrays. Define a subclass Highest to display the names of the students obtaining the highest mark 

The details of the members of both classes are given below:

Class name: Record

Data member/instance variable:

n[] : array to store names
m[]: array to store marks
size: to store the number of students

Member functions/methods:

Record(int cap): parameterized constructor to initialize the data member
size = cap

void readarray() : to enter elements in both the arrays

void display() : displays the array elements

Class name: Highest

Data member/instance variable:

ind: to store the index

Member functions/methods:

Highest(…): parameterized constructor to initialize the data members of both the classes

void find(): finds the index of the student obtaining the highest mark and assign it to ‘ind’

void display(): displays the array elements along with the names and marks of the students who have obtained the highest mark

Assume that the superclass Record has been defined. Using the concept of inheritance, specify the class Highest giving the details of the constructor(…), void find() and void display().

The superclass, main function and algorithm need NOT be written.
Solution:
import java.util.*;
class Record
{
 String n[];
 int m[];
 int size;
public Record(int cap) 
{
    size=cap;
    n=new String[size];
    m=new int[size];
}
public void readarray() 
{
    Scanner sc = new Scanner(System.in);
    System.out.println("Enter names : ");
    for(int i=0;i < size;i++)
    {
        n[i]= sc.next();
    }

    System.out.println("Enter marks : ");

    for(int i= 0;i < size;i++)
    {
        m[i]= sc.nextInt();
    }
}
public void display() 
{
    for(int i=0;i < size;i++)
    {
        System.out.print(n[i] + " ");
    }

    System.out.println();
    for(int i=0;i < size;i++)
    {
        System.out.print(m[i] + " ");
    }
    System.out.println();

}
}

class Highest extends Record
{ 
int ind;
Highest(int cap)
{ super(cap);
  ind=-1;
}
void find()
{ 
readarray();
int hm=m[0];
for (int i=0;ihm)
   { 
    hm=m[i];
    ind=i;
    } 
 } 
}
public void display()
  { 
    super.display();
    for(int i=0;i < size;i++)
   { 
    if(m[i] == m[ind])
    {
     System.out.println(" Highest obtained by " +n[i] + " marks " +m[i]);
    }
   }
  }
}

class rec
{
    public static void main(String args[])
    {
     Highest obj = new Highest(5);
     obj.find();
     obj.display();
    }
}



Question 11 

A linear data structure enables the user to add an address from rear end and remove address from front. Define a class Diary with the following details :

Class name: Diary

Data members/instance variables:

Q[]: array to store the addresses
size: stores the maximum capacity of the array
start: to point the index of the front end
end: to point the index of the rear end

Member functions:

Diary(int max): constructor to initialize the data member size = max, start=0 and end=0

void pushadd(String n): to add the address in the diary from the rear end if possible, otherwise display the message “NO SPACE”

String popadd(): removes and returns the address from the front end of the diary if any, else returns “?????”

void show (): displays all the addresses in the diary

(a) Specify the class Diary giving details of the functions void pushadd(String) and String popadd(). Assume that the other functions have been defined.

The main function and algorithm need NOT be written.

(b) Name the entity used in the above data structure arrangement.
Solution:

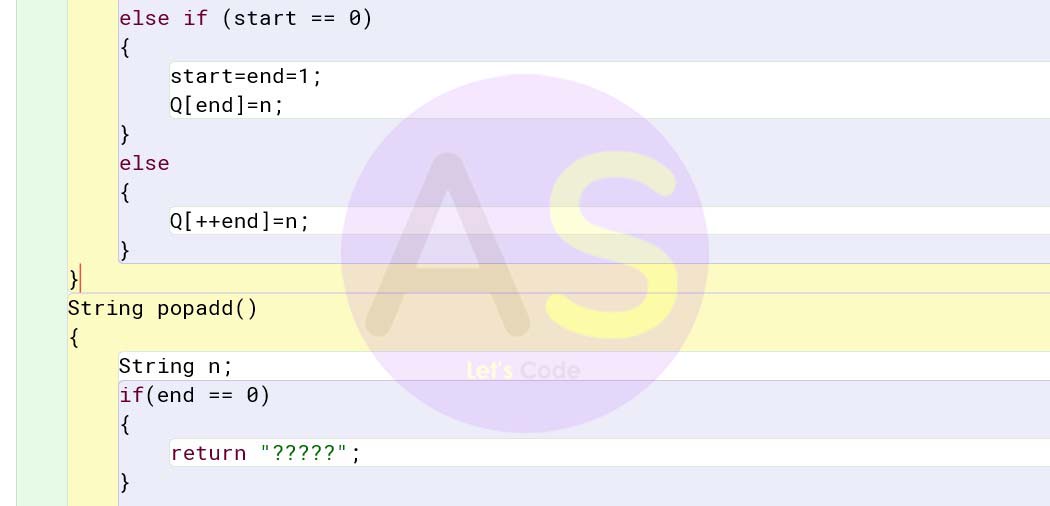
public class Diary
{ 
    String Q[];
    int size,start,end;
    public Diary(int max){
        size=max;
        Q=new String[size];
        start=end=0;
    }

    void pushadd(String n)
    { 
        if(end == size-1)
        {
            System.out.println("NO SPACE");
        }
        else if (start == 0)
        {
            
            start=end=1;
            Q[end]=n;
        }
        else
        {
            Q[++end]=n;
        }
    }

    String popadd()
    { 
        String n;
        if(end == 0)
        {
            return "?????";
        }
        
        else if(start == end)
        {
            n=Q[start];
            start=end=0;
        }
        else
        {
            n=Q[start++];
        }
        return n;
    }
}



Question 12 

(a) A linked list is formed from the objects of the class Node. The class structure of the Node is given below:
    class Node
    {
        int num;
        Node link;
    }

Write an Algorithm OR a Method to find and display the sum of even integers from an existing linked list.

The method declaration is as follows:

void SumEvenNode(Node str)

(b) Answer the following questions from the diagram of a Binary Tree given below:



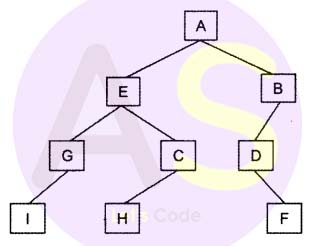(i) Write the pre-order traversal of the above tree structure. 
(ii) State the size of the tree. 
(iii) Name the siblings of the nodes E and G
Solution:
ALGORITHM

Step 1:Start
Step 2: Declare a temporary node, pe <-- str and declare c <-- 0
Step 3: Repeat steps 4 and 5 until P reaches null
Step 4: If p.num % 2 =0 then c<-- c+ p.num
Step 5: move p to next node
Step 6: Print "Sum of even integers" is c
Step 7: End

OR
Method: 
    void SumEvenNode(Node str)
    {
        Node p=str;
        int c=0; 
        while(p != null) 
        {
            if(p.num%2 ==0)
            c +=p.num;
            p=p.next;
        }
        System.out.println("Sum of even integers:" +c);
    }
(b) (i) A E G I C H B D F
(ii) 9
(iii) Sibling of node E is B and sibling of node G is C.


Contact Us

REACH US

SERVICES

  • CODING
  • ON-LINE PREPARATION
  • JAVA & PYTHON

ADDRESS

B-54, Krishna Bhawan, Parag Narain Road, Near Butler Palace Colony Lucknow
Contact:+ 919839520987
Email:info@alexsir.com