Class 12 ISC- Java
Class 12th Java aims to empower students by enabling them to build their own applications introducing some effective tools to enable them to enhance their knowledge, broaden horizons, foster creativity, improve the quality of work and increase efficiency.
It also develops logical and analytical thinking so that they can easily solve interactive programs. Students learn fundamental concepts of computing using object oriented approach in one computer language with a clear idea of ethical issues involved in the field of computing
Class 12th java topics includes revision of class 11th, constructors, user-defined methods, objects and classes, library classes , etc.
Boolean Laws & Expressions
Boolean Algebra
It is a category of algebra in which the variable can have only two walrus i.e. O and 1. It is used
to analyze and simplify digital circuits.
Truth Table
It is a table which represents all the possible input values of logical variables along with all the possible results of the given input values.
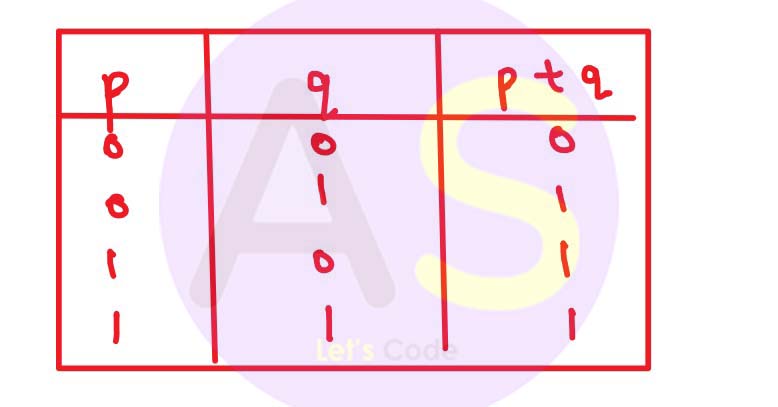
Truth Table for 2 variables :
- 22 = 4 combinations of 0 and 1

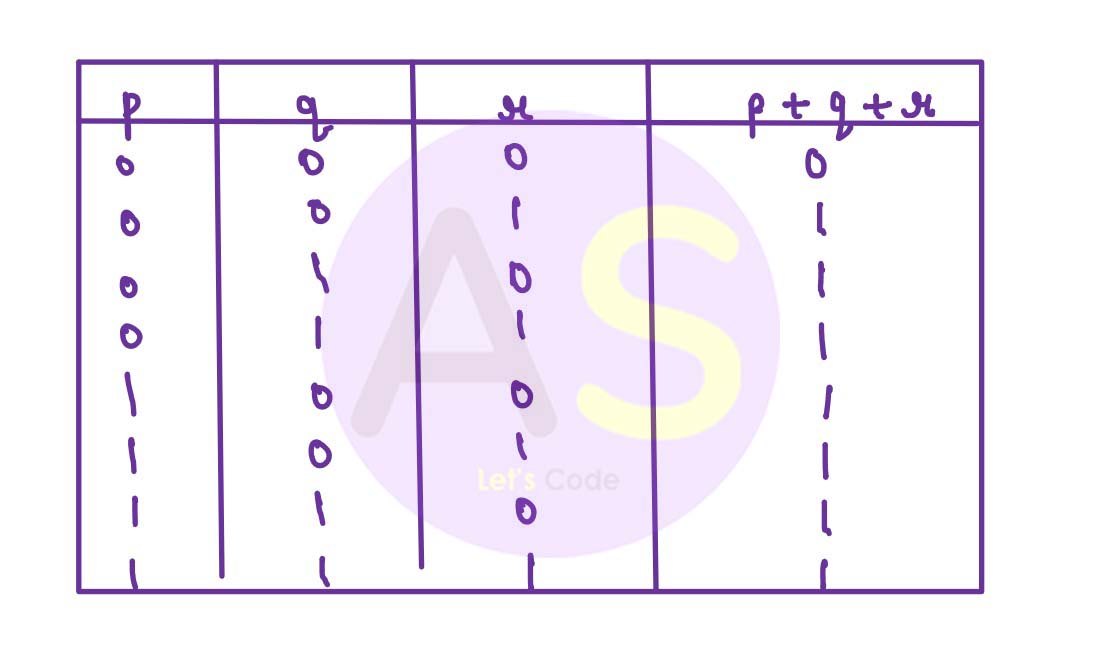
Truth Table for 3 variables :
- 23 = 8 combinations of 0 and 1

Boolean Algebra Laws
Property of 0 :
- A .0 = 0
A + 0 = A
Property of 1 :
- A + 1 = 1
A . 1 = A
Idempotence Law :
- A. A = A
A + A = A
Involution Law :
- Ā̄ = A
Complementary Law :
- A + Ā = 1
A . Ā = 0
Commutative Law :
- A. B = B. A
A + B = B + A
Associative Law :
- ( A. B ). C = A . ( B . C )
( A + B ) + C = A + ( B + C)
Distributive Law :
- A. ( B + C) = A. B + A. C
A + (B. C) = (A + B) . ( A + C)
Absorption Law :
- A. ( A + B) = A
A + (A. B) = A
De-Morgan's Law (Break the line change the sign) :
- (A + B) = Ā . B̄
(A . B) = Ā + B̄
Property of 0 :
- A .0 = 0
A + 0 = A
Property of 1 :
- A + 1 = 1
A . 1 = A
Idempotence Law :
- A. A = A
A + A = A
Involution Law :
- Ā̄ = A
Complementary Law :
- A + Ā = 1
A . Ā = 0
Commutative Law :
- A. B = B. A
A + B = B + A
Associative Law :
- ( A. B ). C = A . ( B . C )
( A + B ) + C = A + ( B + C)
Distributive Law :
- A. ( B + C) = A. B + A. C
A + (B. C) = (A + B) . ( A + C)
Absorption Law :
- A. ( A + B) = A
A + (A. B) = A
De-Morgan's Law (Break the line change the sign) :
- (A + B) = Ā . B̄
(A . B) = Ā + B̄
Some Practice Questions
1. (A + C).(A + AD) + AC + C
= (A + C).(A + AD) + AC + C
= (A + C).(A + AD) + C(1 + A) [PROPERTY OF 1]
= (A + C).(A + AD) + C [ABSORPTION LAW]
= (A + C) . AC [DISTRIBUTIVE LAW]
= AC + AC [IDEMPOTENCE LAW]
= AC
2. A.(A' + B) . C(A + B)
= A.(A' + B) . C(A + B) [DISTRIBUTIVE LAW]
= (A.A' + AB).(AC + BC) [COMPLEMEMTARY LAW]
= (0 + AB).(AC + BC) [PROPERTY OF 0 , DISTRIBUTIVE LAW]
= (ABC)+(ABC) [IDEMPOTENCE LAW]
= ABC
3. XYZ + XY'Z + XYZ' = X (Y + Z)
L.H.S
= XZ(Y + Y') + XYZ' [COMPLEMETARY LAW]
= XZ + XYZ'
= X(Z + YZ') [DISTRIBUTIVE LAW]
= X((Z + Z').(Y +Z)) [COMPLEMETARY LAW]
= X(Y + Z)
4. X'Y'Z' + X'Y'Z + X'YZ + X'YZ' + XY'Z' + XY'Z = X' + Y'
LHS
= X'Y'(Z' + Z) + X'Y (Z + Z') + XY'(Z' + Z) [COMPLEMENTARY LAW]
= X'Y' + X'Y + XY'
= X'(Y' + Y) + XY'[COMPLEMENTARY LAW]
= X' + XY' [DISTRIBUTIVE LAW]
= (X' + X).(X' + Y') [COMPLEMENTARY LAW]
5. ((AB)'' + A' + AB)'
= ((AB)'' + A' + AB)' [DE-MORGAN'S ;LAW]
= ((AB)')' . (A')' . (AB)' [INVOLUTION LAW, DE-MORGAN'S LAW]
= AB . A . A' + B'
= AB . A . A' + B' [DISTRIBUTIVE LAW]
= AB . (AA' + AB') [COMPLEMENTARY LAW]
= AB.AB' [COMPLEMENTARY LAW]
= 0
1. (A + C).(A + AD) + AC + C
= (A + C).(A + AD) + AC + C
= (A + C).(A + AD) + C(1 + A) [PROPERTY OF 1]
= (A + C).(A + AD) + C [ABSORPTION LAW]
= (A + C) . AC [DISTRIBUTIVE LAW]
= AC + AC [IDEMPOTENCE LAW]
= AC
2. A.(A' + B) . C(A + B)
= A.(A' + B) . C(A + B) [DISTRIBUTIVE LAW]
= (A.A' + AB).(AC + BC) [COMPLEMEMTARY LAW]
= (0 + AB).(AC + BC) [PROPERTY OF 0 , DISTRIBUTIVE LAW]
= (ABC)+(ABC) [IDEMPOTENCE LAW]
= ABC
3. XYZ + XY'Z + XYZ' = X (Y + Z)
L.H.S
= XZ(Y + Y') + XYZ' [COMPLEMETARY LAW]
= XZ + XYZ'
= X(Z + YZ') [DISTRIBUTIVE LAW]
= X((Z + Z').(Y +Z)) [COMPLEMETARY LAW]
= X(Y + Z)
4. X'Y'Z' + X'Y'Z + X'YZ + X'YZ' + XY'Z' + XY'Z = X' + Y'
LHS
= X'Y'(Z' + Z) + X'Y (Z + Z') + XY'(Z' + Z) [COMPLEMENTARY LAW]
= X'Y' + X'Y + XY'
= X'(Y' + Y) + XY'[COMPLEMENTARY LAW]
= X' + XY' [DISTRIBUTIVE LAW]
= (X' + X).(X' + Y') [COMPLEMENTARY LAW]
5. ((AB)'' + A' + AB)'
= ((AB)'' + A' + AB)' [DE-MORGAN'S ;LAW]
= ((AB)')' . (A')' . (AB)' [INVOLUTION LAW, DE-MORGAN'S LAW]
= AB . A . A' + B'
= AB . A . A' + B' [DISTRIBUTIVE LAW]
= AB . (AA' + AB') [COMPLEMENTARY LAW]
= AB.AB' [COMPLEMENTARY LAW]
= 0
Boolean Expressions
Boolean expressions can be written in two forms :
1. Sum of Product Form (SOP) : It means sum of producted terms.
Example : AB + BC
2. Product of Sum Form (POS) : It means product of sum terms.
Example : (A + B) . ( B + C')
Canonical SOP Expression :
When a boolean expression is represented entirely as a sum of minterms it is known as canonical SOP expression.
Example : A'BC + ABC' + ABC
Canonical POS Expression :
When a boolean expression is represented entirely as a product of maxterms it is known as canonical POS expression.
Example : (A + B' + C) . (A + B' + C') . (A + B + C)
Minterm :
Product of all variables present with or without bar is termed as minterm [bar applied on 0] i.e. A' = 0 , A = 1. It is represented with (m)
Maxterm :
Sum of all variables present with or without bar is termed as maxterm [bar applied on 1] i.e. A' = 1 , A = 0. It is represented with (M)
Convert the following expression into canonical SOP form : X + Y'Z

Convert the following expression into canonical POS form : X'Y + YZ'


Convert the following canonical SOP expression into canonical POS form : F(X,Y,Z) = ∑(1, 4, 5, 6, 7)

Convert the following canonical POS expression into canonical SOP form : F(X,Y,Z) = π(0, 1, 4, 5, 7)

1. Sum of Product Form (SOP) : It means sum of producted terms.
Example : AB + BC
2. Product of Sum Form (POS) : It means product of sum terms.
Example : (A + B) . ( B + C')
Example : A'BC + ABC' + ABC
Example : (A + B' + C) . (A + B' + C') . (A + B + C)
Convert the following expression into canonical SOP form : X + Y'Z

Convert the following expression into canonical POS form : X'Y + YZ'


Convert the following canonical SOP expression into canonical POS form : F(X,Y,Z) = ∑(1, 4, 5, 6, 7)

Convert the following canonical POS expression into canonical SOP form : F(X,Y,Z) = π(0, 1, 4, 5, 7)
