Class 12 ISC- Java
Class 12th Java aims to empower students by enabling them to build their own applications introducing some effective tools to enable them to enhance their knowledge, broaden horizons, foster creativity, improve the quality of work and increase efficiency.
It also develops logical and analytical thinking so that they can easily solve interactive programs. Students learn fundamental concepts of computing using object oriented approach in one computer language with a clear idea of ethical issues involved in the field of computing
Class 12th java topics includes revision of class 11th, constructors, user-defined methods, objects and classes, library classes , etc.
Address Calculation
Address Calculation in Single-Dimensional Array
-
As we have learned about single dimensional array that,it stores the data in a single row only.
-
Here, each array element in a linear array is stored in specific address in memory,to access these
array
elements
there is a single subscript which can be row or column subscript,by these subscript we can access
the array elements.
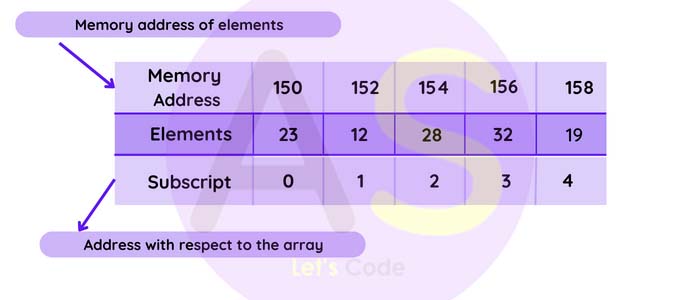
In the above diagram ,there is a linear array with 5 elements which is stored in a memory address
starting from 150.And to access these array elements we use array subscript which starts from 0
Now to find the memory address of any array element the formula used is:-
Address of A[I](Element whose address is to calculated)=B+W*(I-LB)
Here,
B=Base Address,this is actual address of 1st element of the array
W=Width,this is storage size of one element in the array
I=It is the subscript of element whose address is to be found
LB=Lower Limit/Lower Bound of subscript,this is the address with respect to array to access its elements,if
not specified assume it as 0(zero)
Now let us understand this formula by examples:-
Example:-
A linear array A[16........30] with base address as 100 and size of each element is 4 bytes.Find the
memory address of A[27]
Solution:
Base address (B)=100
Width(W)=4
Subset of element whose address to be found(I)=27
Lower Bound(LB)=16
Formula used:
A[I]=B+W*(I-LB)
Address of A[27]=100+4*(27-16)
=100+4*11
=144[Ans]
Here,
B=Base Address,this is actual address of 1st element of the array
W=Width,this is storage size of one element in the array
I=It is the subscript of element whose address is to be found
LB=Lower Limit/Lower Bound of subscript,this is the address with respect to array to access its elements,if not specified assume it as 0(zero)
Base address (B)=100
Width(W)=4
Subset of element whose address to be found(I)=27
Lower Bound(LB)=16
Formula used:
A[I]=B+W*(I-LB)
A[I]=B+W*(I-LB)
Address of A[27]=100+4*(27-16)
=100+4*11
=144[Ans]
Address Calculation in Double-Dimensional Array
-
When we talk about Double-Dimensional array,it is like a matrix which is composed of rows and
columns
-
It is represent by A[X][Y],where X is number of rows and Y is number of columns
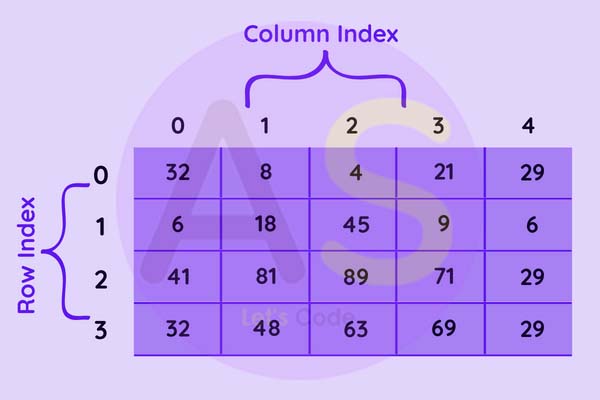
In a memory the double dimensional array elements are stored in a linearized way,which enables array to
store its data.
There are two alternatives to achieve this linearization which are:
-
Row-Major
- Column-Major
Row Major
When the elements of double dimensional array is stored in row form ,then it is called row major
Let us understand this concept by a diagram:
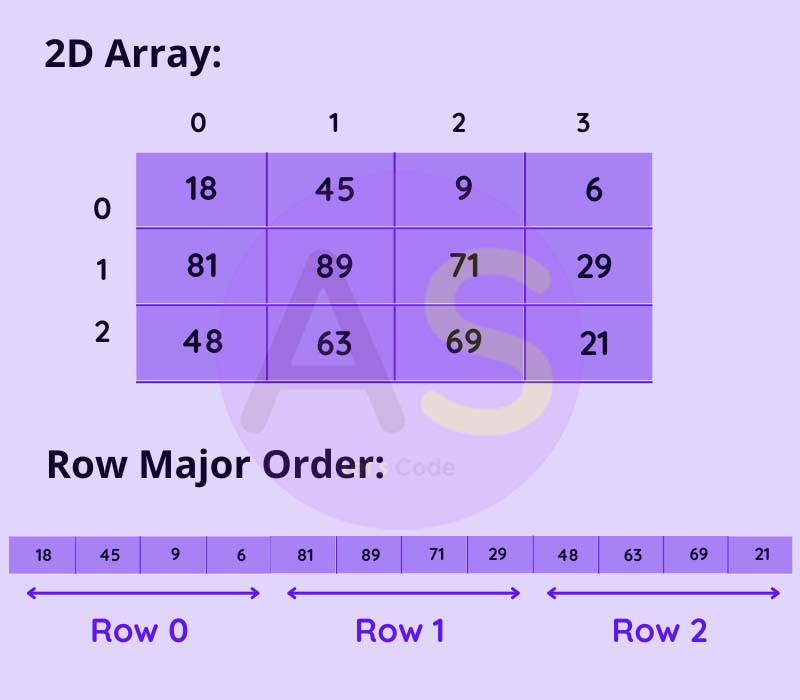
Formula to calculate the memory address of any array element in row major format is:
Address of A[I][J[(Element whose address is to calculated)=B+W*[N*(I-Lr)+(J-Lc)]
Here,
B=Base Addres
W=Storage size of one element stored in the array
N=Number of column of the given matrizx
I=Row subscript of element whose address to be found
J=Column subscript of element whose address to be found
Lr=Lower Limit of row index of matrix
Lc=Lower limit of column index of matrix
Here,
B=Base Addres
W=Storage size of one element stored in the array
N=Number of column of the given matrizx
I=Row subscript of element whose address to be found
J=Column subscript of element whose address to be found
Lr=Lower Limit of row index of matrix
Lc=Lower limit of column index of matrix
Column Major
When the elements of double dimensional array is stored in column form ,then it is called column major
Let us understand this concept by a diagram:
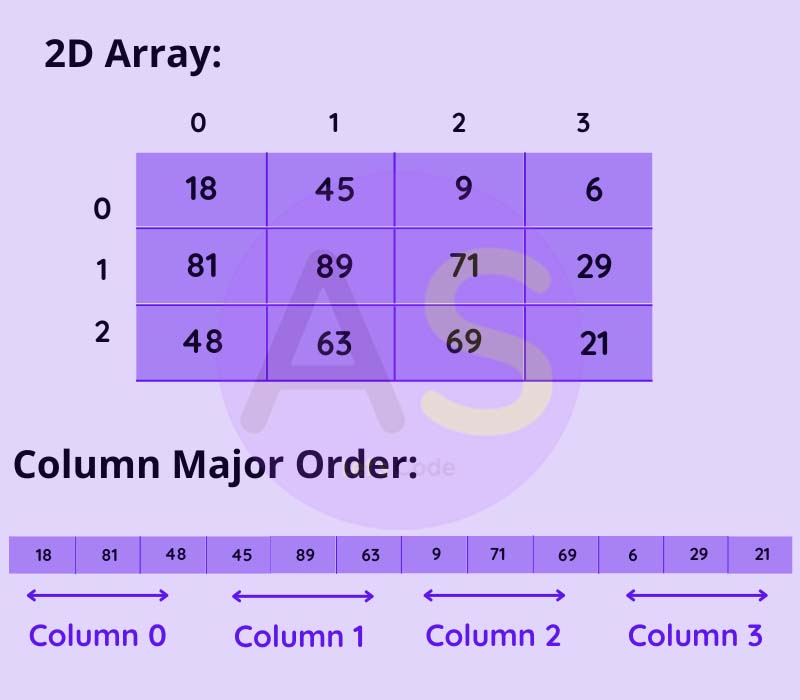
Formula to calculate the memory address of any array element in column major format is:
Address of A[I][J](Element whose address is to calculated)=B+W*[M*(J-Lc)+(I-Lr)]
Here,
B=Base Addres
W=Storage size of one element stored in the array
M=Number of rows of the given matrizx
I=Row subscript of element whose address to be found
J=Column subscript of element whose address to be found
Lr=Lower Limit of row index of matrix
Lc=Lower limit of column index of matrix
Now Let us see examples of address calculation of 1-D and 2-D array:
Example 1(ISC 2016 Question):-
A matrix A[m] [n] is stored with each element requiring 4 bytes of storage. If the base address at A[1]
[1] is 1500 and the address at A [4] [5] is 1608, determine the number of rows of the matrix when the
matrix is stored in Column Major Wise.
Solution:
address of A[I][J]=1608
Base address (B)=1500
Width(W)=4
Column subscript of A[I][J] (J)=5
Row subscript of A[I][J] (I)=4
Lower limit of row index (Lr)=1
Lower limit of column index (Lc)=1
Find Number of matrix(M)?
Formula used:
Column Major A[I][J]=B+W*[M*(J-Lc)+(I-Lr)]
On,putting values
1608=1500+4[M*(5-1)+(4-1)]
1608=1500+16*M+12
1608=1512+16M
16M=96
SO No of rows in a matrix (M) is 6
Example 2(ISC 2017 Question):-
A matrix P[15][10] is stored with each element requiring 8 bytes of storage. If the base
address at P[0][0] is 1400, determine the address at P[10][7] when the matrix is stored in
Row Major Wise.
Solution:
Base address (B)=1400
Width(W)=8
Column subscript whose address is to be found (J)=7
Row subscript whose address is to be found (I)=10
Lower limit of row index (Lr)=0
Lower limit of column index (Lc)=0
No of Columns (N)=10
Find Address of array element P[10][7]
Formula used:
Address of P[I][J[(Element whose address is to calculated)=B+W*[N*(I-Lr)+(J-Lc)]
On,putting values
P[10][7]=1400+8[(10-0)*10+(7-0)]
P[10][7]=1400+8[100+7]
P[10][7]=1400+857
Address of P[10][7] is 2256
Example 3(ISC 2018 Question):-
A matrix A[m][m] is stored in the memory with each element requiring 4 bytes of
storage. If the base address at A [1][1] is 1500 and address of A [4][5] is 1608,
determine the order of matrix when it is stored in Column Major Wise.
Solution:
Address of A[I][J]=1608
Base address (B)=1500
Width(W)=4
Column subscript whose address is to be found (J)=5
Row subscript whose address is to be found (I)=4
Lower limit of row index (Lr)=1
Lower limit of column index (Lc)=1
Find Number of rows (M)?
Formula used:
Column Major A[I][J]=B+W*[M*(J-Lc)+(I-Lr)]
On,putting values
1608=1500+4[(5-1)*M +(4-1)]
1608=1500+4[4M+3]
1608=1500+16M+12
1608=1512+16M
Number of rows in a matrix is 6
Example 4(ISC 2019 Question):-
A matrix ARR[ – 4...6, 3....8] is stored in the memory with each element requiring
4 bytes of storage. If the base address is 1430, find the address of ARR[3][6] when
the matrix is stored in Row Major Wise.
Solution:
Base address (B)=1430
Width(W)=4
Column subscript whose address is to be found (J)=6
Row subscript whose address is to be found (I)=3
Lower limit of row index (Lr)=-4
Lower limit of column index (Lc)=3
Number of columns(N)=6
Find the address of array element A[3][6]
Formula used:
Address of P[I][J[(Element whose address is to calculated)=B+W*[N*(I-Lr)+(J-Lc)]
On putting values,
A[3][6]=1430+4[3-(-4)*6+(6-3)]
A[3][6]=1430+4[42+3]
A[3][6]=1430+180
Address of array element A[3][6]=1610
Example 5(ISC 2020 Question):-
A matrix B[10][20] is stored in the memory with each element requiring 2 bytes of
storage. If the base address at B[2][1] is 2140, find the address of B[5][4] when the
matrix is stored in Column Major Wise.
Solution:
Base address (B)=2140
Width(W)=2
Column subscript whose address is to be found (J)=4
Row subscript whose address is to be found (I)=5
Lower limit of row index (Lr)=2
Lower limit of column index (Lc)=1
Number of rows(M)=10
Find the address of array element A[5][4]
Formula used:
Address of A[I][J](Element whose address is to calculated)=B+W*[M*(J-Lc)+(I-Lr)]
On putting values,
A[5][4]=2140+2[(4-1)*10 +(5-2)]
A[5][4]=2140+2[33]
A[5][4]=2140+66
Address of array element A[5][4] is 2206
Here,
B=Base Addres
W=Storage size of one element stored in the array
M=Number of rows of the given matrizx
I=Row subscript of element whose address to be found
J=Column subscript of element whose address to be found
Lr=Lower Limit of row index of matrix
Lc=Lower limit of column index of matrix
address of A[I][J]=1608
Base address (B)=1500
Width(W)=4
Column subscript of A[I][J] (J)=5
Row subscript of A[I][J] (I)=4
Lower limit of row index (Lr)=1
Lower limit of column index (Lc)=1
Find Number of matrix(M)?
Formula used:
Column Major A[I][J]=B+W*[M*(J-Lc)+(I-Lr)]
Column Major A[I][J]=B+W*[M*(J-Lc)+(I-Lr)]
On,putting values
1608=1500+4[M*(5-1)+(4-1)]
1608=1500+16*M+12
1608=1512+16M
16M=96
SO No of rows in a matrix (M) is 6
Base address (B)=1400
Width(W)=8
Column subscript whose address is to be found (J)=7
Row subscript whose address is to be found (I)=10
Lower limit of row index (Lr)=0
Lower limit of column index (Lc)=0
No of Columns (N)=10
Find Address of array element P[10][7]
Formula used:
Address of P[I][J[(Element whose address is to calculated)=B+W*[N*(I-Lr)+(J-Lc)]
Address of P[I][J[(Element whose address is to calculated)=B+W*[N*(I-Lr)+(J-Lc)]
On,putting values
P[10][7]=1400+8[(10-0)*10+(7-0)]
P[10][7]=1400+8[100+7]
P[10][7]=1400+857
Address of P[10][7] is 2256
Address of A[I][J]=1608
Base address (B)=1500
Width(W)=4
Column subscript whose address is to be found (J)=5
Row subscript whose address is to be found (I)=4
Lower limit of row index (Lr)=1
Lower limit of column index (Lc)=1
Find Number of rows (M)?
Formula used:
Column Major A[I][J]=B+W*[M*(J-Lc)+(I-Lr)]
Column Major A[I][J]=B+W*[M*(J-Lc)+(I-Lr)]
On,putting values
1608=1500+4[(5-1)*M +(4-1)]
1608=1500+4[4M+3]
1608=1500+16M+12
1608=1512+16M
Number of rows in a matrix is 6
Base address (B)=1430
Width(W)=4
Column subscript whose address is to be found (J)=6
Row subscript whose address is to be found (I)=3
Lower limit of row index (Lr)=-4
Lower limit of column index (Lc)=3
Number of columns(N)=6
Find the address of array element A[3][6]
Formula used:
Address of P[I][J[(Element whose address is to calculated)=B+W*[N*(I-Lr)+(J-Lc)]
Address of P[I][J[(Element whose address is to calculated)=B+W*[N*(I-Lr)+(J-Lc)]
On putting values,
A[3][6]=1430+4[3-(-4)*6+(6-3)]
A[3][6]=1430+4[42+3]
A[3][6]=1430+180
Address of array element A[3][6]=1610
Base address (B)=2140
Width(W)=2
Column subscript whose address is to be found (J)=4
Row subscript whose address is to be found (I)=5
Lower limit of row index (Lr)=2
Lower limit of column index (Lc)=1
Number of rows(M)=10
Find the address of array element A[5][4]
Formula used:
Address of A[I][J](Element whose address is to calculated)=B+W*[M*(J-Lc)+(I-Lr)]
Address of A[I][J](Element whose address is to calculated)=B+W*[M*(J-Lc)+(I-Lr)]
On putting values,
A[5][4]=2140+2[(4-1)*10 +(5-2)]
A[5][4]=2140+2[33]
A[5][4]=2140+66
Address of array element A[5][4] is 2206
Contact Us
REACH US
SERVICES
- CODING
- ON-LINE PREPARATION
- JAVA & PYTHON
ADDRESS
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+ 919839520987
Email:info@alexsir.com