Class 11 ISC- Java
Class11 computer applications is designed to promote the study of computer languages, their use to build applications, to understand the user’s responsibility, the protocol, and the ethical issues related to the field of computing.
Java in class 11 for isc is very handy when it comes to practice on computers but for the beginers there might be some errors and problems such as exception. But it's always advisable to practice program on computer than writing it on paper because it cherishes your practical skills , knowledge and typing speed and you'll come to know new things and if you want to be a software developer someday then its a must call for you.
Class 11th java topics includes revision of class 11th, numbers,Encoding,Propositional Logic, Memory, Objects, Datatypes, variables, etc.
Number Conversions
Binary number system is the most important one in digital system as it is very easy to implement in circuitry. The decimal system is important because it is universally used to represent quantities outside of digital system. In addition to these number systems, octal and hexadecimal number system find widespread application in digital system.
There are ten types of number conversions listed below :
- Decimal to Binary
- Binary to Decimal
- Decimal to Hexadecimal
- Decimal to Octal
- Binary to Hexadecimal
- Binary to Octal
- Hexadecimal to Decimal
- Octal to Decimal
- Hexadecimal to Binary
- Octal to Binary
Decimal to Binary
Repeatedly divide the decimal number by 2 until the quotient becomes 1 and record all the remainders. The remainders should be written from bottom to upwards to get the binary equivalent of the decimal number.


Binary to Decimal
To obtain the decimal equivalent of a binary number, individual digits of binary number should be multiplied by powers of 2 starting with the rightmost digit multiplied by 20 , second last digit multiplied by 21 , third last digit multiplied by 22 and so on up to the leftmost digit. For digits after the decimal point, the leftmost digit should be multiplied by 2-1 and the next digit by 2-2 and so on up to the rightmost digit.


Binary to Octal
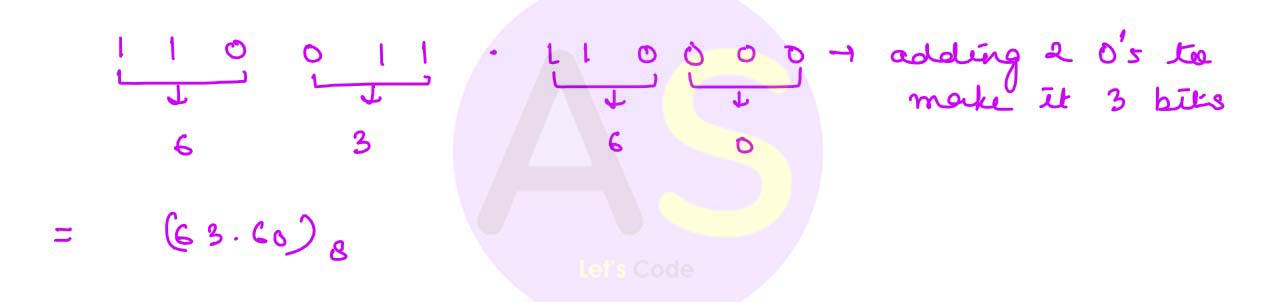
To obtain the octal equivalent of a binary number, digits of binary number should be divided into groups of three digits starting from the rightmost digit for the integer part and starting from the leftmost digit for the fractional part. Convert each group of 3 digits to one octal digit.
Note: 1 or 2 zeroes can be added before the leftmost digit or after the rightmost digit to make a complete group of 3 bits.



Binary to Hexadecimal
To obtain the Hexadecimal equivalent of a binary number, digits of binary number should be divided into groups of four digits starting from the rightmost digit for the integer part and starting from the leftmost digit for the fractional part. Convert each group of 4 digits to one hexadecimal digit .
Note: 1,2 or 3 zeroes can be added before the leftmost digit or after the rightmost digit to make a complete group of 4 bits.




Hexadecimal to Binary
To obtain the binary equivalent of a hexadecimal number, individual digits of the hexadecimal number should be converted to binary in groups of four digits


Octal to Binary
To obtain the binary equivalent of a octal number, individual digits of the octal number should be converted to binary in groups of three digits


Decimal to Octal
Repeatedly divide the decimal number by 8 until the quotient becomes less than 8 and record all the remainders. The remainders should be written bottom to upwards to get the octal equivalent of the decimal number.


Decimal to Hexadecimal
Repeatedly divide the decimal number by 16 until the quotient becomes less than 16 and record all the remainders. The remainders should be written bottom to upwards to get the hexadecimal equivalent of the decimal number. Here,
• 10=A
• 11=B
• 12=C
• 13=D
• 14=E
• 15=F


Hexadecimal to Decimal
To obtain decimal equivalent of hexadecimal number you should convert it to its binary equivalent, to obtain the binary equivalent of a hexadecimal number, individual digits of the hexadecimal number should be converted to binary in groups of four digits
After this convert this binary number to its decimal equivalent , to obtain the decimal equivalent of a binary number, individual digits of binary number should be multiplied by powers of 2 starting with the rightmost digit multiplied by 20 , second last digit multiplied by 21 , third last digit multiplied by 22 and so on up to the leftmost digit. For digits after the decimal point, the leftmost digit should be multiplied by 2-1 and the next digit by 2-2 and so on up to the rightmost digit.






Octal to Decimal
To obtain decimal equivalent of octal number you should convert it to its binary equivalent, to obtain the binary equivalent of a octal number, individual digits of the octal number should be converted to binary in groups of three digits.
After this convert this binary number to its decimal equivalent , to obtain the decimal equivalent of a binary number, individual digits of binary number should be multiplied by powers of 2 starting with the rightmost digit multiplied by 20 , second last digit multiplied by 21 , third last digit multiplied by 22 and so on up to the leftmost digit. For digits after the decimal point, the leftmost digit should be multiplied by 2-1 and the next digit by 2-2 and so on up to the rightmost digit.



